



Next: 5 Conclusions.
Up: 4 Alternate Theories.
Previous: 4.1 Completeness.
1) 

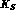 evolution. Processes that imply such an
evolution affect the
evolution. Processes that imply such an
evolution affect the  --decay time distribution.
Let
--decay time distribution.
Let 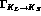 be the rate of incoherent evolution of
be the rate of incoherent evolution of 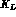 \
into
\
into 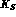 . In the experimental setup of Sect. 2,
a fraction
. In the experimental setup of Sect. 2,
a fraction 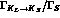 of incoherent
of incoherent 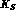 would
be present all the time alongside with the
would
be present all the time alongside with the 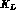 mesons,
in equilibrium, i.e. with as many
mesons,
in equilibrium, i.e. with as many 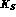 being formed and decaying
per unit of time.
Each one of these
being formed and decaying
per unit of time.
Each one of these 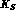 would decay into
would decay into 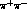 \
at a rate equal to
\
at a rate equal to  instead of
instead of 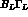 for
for  .
Thus the coefficient
.
Thus the coefficient  of
of 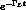 in Eq. (4)
would be increased, without
in Eq. (4)
would be increased, without  and
and  being appreciably changed.
Thus
being appreciably changed.
Thus  of Eq. (5) is not zero anymore, and one can deduce
of Eq. (5) is not zero anymore, and one can deduce

The test of Ref. [2] yields
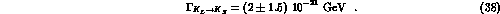
Note that  is equivalent to
the parameter
is equivalent to
the parameter  of Refs. [9] and [10]
in the context of their theory.
of Refs. [9] and [10]
in the context of their theory.
In the test of Sect. 3.2 that relies on the  --decay distribution,
the incoherent
--decay distribution,
the incoherent 

 process would act on the
process would act on the  of the
of the 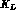
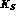 and
and 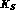
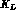 systems and produce
systems and produce 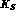
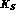 states after some time. As an
average in the sample of events
states after some time. As an
average in the sample of events

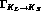 can be derived from
can be derived from 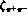 by the same relation as Eq. (37) for
by the same relation as Eq. (37) for  . At Da
. At Da ne , we can hope to get
an upper limit of the order of 1/10 ms, i.e. 10
ne , we can hope to get
an upper limit of the order of 1/10 ms, i.e. 10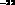 GeV.
GeV.

2) 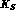
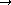
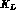 evolution. Such process would produce
evolution. Such process would produce 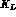
 events
in the test of Sect. 3.3.
events
in the test of Sect. 3.3.
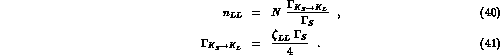
Suppose that the uncertainty about the background in the test of Sect. 3.3
is, let us say, 100 times the contribution of the 

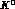
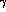 events,
i.e. 10
events,
i.e. 10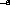 , then one could still detect
values of
, then one could still detect
values of 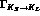 as low as 1/100
as low as 1/100 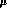 s or 10
s or 10 GeV.
GeV.
3) Evolution 
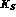 --
--
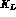 into
into 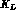
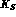
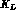 . This
evolution can be expressed also as
. This
evolution can be expressed also as

It will produce states where both kaons can decay into  or both
into
or both
into  at the same time. Let us call
at the same time. Let us call  the rate of this process. For the tests of Sect. 3.2 involving
the rate of this process. For the tests of Sect. 3.2 involving
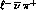 or
or 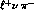 ,
,

Using the estimate of Eq. (29), we could explore values of
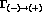 lower than 1/0.1 ms,
i.e. 10
lower than 1/0.1 ms,
i.e. 10 GeV.
GeV.
If a violation of quantum mechanics is ever revealed by one
of the tests above, comparing the amount of
violation found in each test will bring information about the
decoherence mechanism responsible for the violation.
Also questions will be raised about the background
due to 
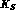 and
and 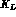
 events produced by
events produced by  --decay
into
--decay
into  , [11].
However, the effect of this background can be
distinguished from the decoherence effects described
in this section by dividing
the sample of events into those where kaons decay near the intersection point
and those where they decay far from it.
In the test where the two kaons decay via the
, [11].
However, the effect of this background can be
distinguished from the decoherence effects described
in this section by dividing
the sample of events into those where kaons decay near the intersection point
and those where they decay far from it.
In the test where the two kaons decay via the
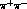 mode, the
mode, the 


 background
populates the bin
background
populates the bin  at z = 0 with more events when
at z = 0 with more events when 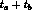 is small than when
is small than when 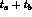 is large,
actually like
is large,
actually like 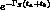 .
On the contrary, the decoherence mechanisms take time to accumulate
events for z = 0; thus
.
On the contrary, the decoherence mechanisms take time to accumulate
events for z = 0; thus  at z = 0
grows as a function of
at z = 0
grows as a function of 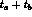 .
.




Next: 5 Conclusions.
Up: 4 Alternate Theories.
Previous: 4.1 Completeness.
Carlos E.Piedrafita


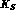 evolution. Processes that imply such an
evolution affect the
evolution. Processes that imply such an
evolution affect the  --decay time distribution.
Let
--decay time distribution.
Let 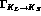 be the rate of incoherent evolution of
be the rate of incoherent evolution of 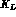 \
into
\
into 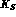 . In the experimental setup of Sect. 2,
a fraction
. In the experimental setup of Sect. 2,
a fraction 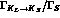 of incoherent
of incoherent 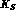 would
be present all the time alongside with the
would
be present all the time alongside with the 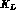 mesons,
in equilibrium, i.e. with as many
mesons,
in equilibrium, i.e. with as many 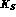 being formed and decaying
per unit of time.
Each one of these
being formed and decaying
per unit of time.
Each one of these 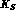 would decay into
would decay into 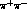 \
at a rate equal to
\
at a rate equal to  instead of
instead of 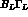 for
for  .
Thus the coefficient
.
Thus the coefficient  of
of 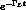 in Eq. (4)
would be increased, without
in Eq. (4)
would be increased, without  and
and 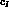 being appreciably changed.
Thus
being appreciably changed.
Thus  of Eq. (5) is not zero anymore, and one can deduce
of Eq. (5) is not zero anymore, and one can deduce

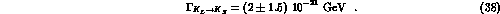
 is equivalent to
the parameter
is equivalent to
the parameter  of Refs. [
of Refs. [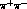 --decay distribution,
the incoherent
--decay distribution,
the incoherent 

 process would act on the
process would act on the 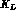 of the
of the 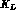
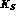 and
and 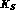
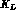 systems and produce
systems and produce 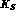
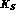 states after some time. As an
average in the sample of events
states after some time. As an
average in the sample of events

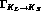 can be derived from
can be derived from 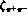 by the same relation as Eq. (
by the same relation as Eq. ( . At Da
. At Da ne , we can hope to get
an upper limit of the order of 1/10 ms, i.e. 10
ne , we can hope to get
an upper limit of the order of 1/10 ms, i.e. 10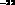 GeV.
GeV.
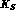
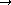
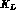 evolution. Such process would produce
evolution. Such process would produce 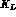
 events
in the test of Sect.
events
in the test of Sect. 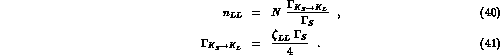


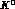
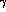 events,
i.e. 10
events,
i.e. 10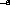 , then one could still detect
values of
, then one could still detect
values of 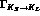 as low as 1/100
as low as 1/100 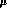 s or 10
s or 10 GeV.
GeV.

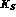 --
--
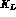 into
into 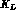
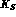
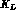 . This
evolution can be expressed also as
. This
evolution can be expressed also as

 or both
into
or both
into  at the same time. Let us call
at the same time. Let us call  the rate of this process. For the tests of Sect.
the rate of this process. For the tests of Sect. 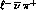 or
or 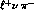 ,
,

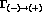 lower than 1/0.1 ms,
i.e. 10
lower than 1/0.1 ms,
i.e. 10 GeV.
GeV.

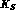 and
and 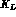
 events produced by
events produced by  --decay
into
--decay
into  , [
, [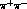 mode, the
mode, the 


 background
populates the bin
background
populates the bin  at z = 0 with more events when
at z = 0 with more events when 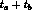 is small than when
is small than when 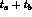 is large,
actually like
is large,
actually like 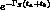 .
On the contrary, the decoherence mechanisms take time to accumulate
events for z = 0; thus
.
On the contrary, the decoherence mechanisms take time to accumulate
events for z = 0; thus  at z = 0
grows as a function of
at z = 0
grows as a function of 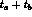 .
.