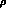 .
In quantum mechanics, the time evolution of
.
In quantum mechanics, the time evolution of 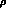 is described
by a unitary transformation,
is described
by a unitary transformation,
The tests above are designed to detect effects described by
alternate theories to quantum mechanics, more specifically
by those which do
not use hidden variables. The maximum information that can characterize
a quantum system is still given by a density matrix 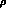 .
In quantum mechanics, the time evolution of
.
In quantum mechanics, the time evolution of 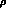 is described
by a unitary transformation,
is described
by a unitary transformation,
from which one can derive a hamiltonian,

Eq. (32) conserves the rank of 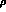 , thus
insures that a pure state cannot evolve into a mixed state.
That is the property tested by our tests of interferences.
In these tests, the initial state is one that quantum mechanics
considers pure and the measurements check that, within error,
the final density matrix is of rank 1, i.e.
has the mathematical property that describes a pure state.
, thus
insures that a pure state cannot evolve into a mixed state.
That is the property tested by our tests of interferences.
In these tests, the initial state is one that quantum mechanics
considers pure and the measurements check that, within error,
the final density matrix is of rank 1, i.e.
has the mathematical property that describes a pure state.