



Next: 3 Two-Kaon Systems.
Up: Chapter 2 Section 1
Previous: 1 Introduction.
Tests of quantum mechanics using 

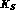 regeneration have been
proposed long ago, [1]. They consist
of transporting a neutral kaon beam over a distance long enough for all
its
regeneration have been
proposed long ago, [1]. They consist
of transporting a neutral kaon beam over a distance long enough for all
its 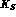 --component to decay; letting it impinge on a piece of material
called regenerator; and recording the number
of decays into two charged pions as a function of distance to that
regenerator.
--component to decay; letting it impinge on a piece of material
called regenerator; and recording the number
of decays into two charged pions as a function of distance to that
regenerator.
There are two processes by which a kaon emerging from the regenerator
in the very forward direction can decay into 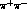 :
:
1) plain transmission of a 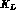 and decay via the CP violating mode;
and decay via the CP violating mode;
2) 
 regeneration followed by a CP conserving decay.
regeneration followed by a CP conserving decay.
The initial  can be considered as a pure state
in each momentum interval, if that interval is small enough.
Because the kaon has spin zero,
all configurations of its
can be considered as a pure state
in each momentum interval, if that interval is small enough.
Because the kaon has spin zero,
all configurations of its  --decays
can be considered as two pions in an S--wave state,
which is a pure state.
Thus, at each momentum, the two-pion state
from the decay of a kaon in the very forward direction is
a pure state. Whether the kaon is transmitted or
coherently regenerated, the state of the regenerator is
the same, after as well as before the kaon traversed it.
Therefore the two processes interfere between one another.
As a function of proper time t, the decay rate can be written
as
--decays
can be considered as two pions in an S--wave state,
which is a pure state.
Thus, at each momentum, the two-pion state
from the decay of a kaon in the very forward direction is
a pure state. Whether the kaon is transmitted or
coherently regenerated, the state of the regenerator is
the same, after as well as before the kaon traversed it.
Therefore the two processes interfere between one another.
As a function of proper time t, the decay rate can be written
as
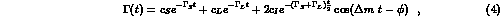
where  and
and 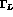 are the total decay rates of the
are the total decay rates of the 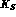 and of the
and of the
 mesons, respectively;
mesons, respectively; 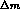 is the
is the  --
--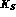 mass difference;
and
mass difference;
and 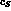 ,
,  ,
, 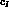 , and
, and  are parameters that
can be measured by the shape of the time distribution
are parameters that
can be measured by the shape of the time distribution 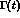 .
.
The third term in Eq. (4) is the interference
term between the two processes.
Quantum theory predicts 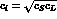 .
In accordance with Eq. (3), we define
.
In accordance with Eq. (3), we define

which measures the amount of violation in the regeneration process.
A test of this kind was performed with neutral kaons of momentum
ranging from 4 to 10 GeV/c and a carbon regenerator, [2].
The result was
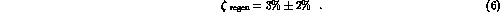
The error was essentially statistical.
The same type of test could be performed at Da ne .
The accuracy would be improved.
For instance, one may surround one of the two intersection points
with a regenerator of a cylindric form, with its axis along the
ne .
The accuracy would be improved.
For instance, one may surround one of the two intersection points
with a regenerator of a cylindric form, with its axis along the 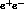 beam
line, with a radius of 20 cm and a height of 20 cm too. The regenerator
would intercept
beam
line, with a radius of 20 cm and a height of 20 cm too. The regenerator
would intercept  emitted within a solid angle of about 5 sr. The
thickness of the cylinder should be adjusted to produce,
just behind the regenerator, more
emitted within a solid angle of about 5 sr. The
thickness of the cylinder should be adjusted to produce,
just behind the regenerator, more  --decays by regenerated
--decays by regenerated 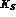 than by transmitted
than by transmitted 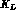 . Then one makes sure that
the
. Then one makes sure that
the 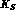 --
--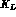 interference pattern visible in the
interference pattern visible in the  --mode is
as long as possible. For instance, a beryllium cylinder 2.4 cm thick
would be an adequate regenerator. It would regenerate one
--mode is
as long as possible. For instance, a beryllium cylinder 2.4 cm thick
would be an adequate regenerator. It would regenerate one  in
10
in
10 according to Ref. [3],
i.e. an appropriate amount of regenerated
according to Ref. [3],
i.e. an appropriate amount of regenerated  .
.
At a luminosity 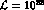 , in one month calendar time with
an efficiency of 30%, i.e. an integrated luminosity of 1000 pb
, in one month calendar time with
an efficiency of 30%, i.e. an integrated luminosity of 1000 pb ,
one may expect more than 10
,
one may expect more than 10
 \
through the regenerator according to Refs. [4]
and [5]. Then the decoherence parameter
\
through the regenerator according to Refs. [4]
and [5]. Then the decoherence parameter  would be measured with
a statistical error of less 1%.
If the angle of the kaon emerging from the regenerator
can be determined to better than 20 mr, the effect of the incoherent
regeneration and elastic scattering should introduce an uncertainty
of less than 1%.
Finally one should to be able to eliminate background
in
would be measured with
a statistical error of less 1%.
If the angle of the kaon emerging from the regenerator
can be determined to better than 20 mr, the effect of the incoherent
regeneration and elastic scattering should introduce an uncertainty
of less than 1%.
Finally one should to be able to eliminate background
in 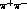 --decays down to less
than 10
--decays down to less
than 10 times the
times the  decay rate into
decay rate into  \
at a machine like Da
\
at a machine like Da ne \
designed to measure the CP violation parameter
called
ne \
designed to measure the CP violation parameter
called 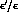 .
Therefore combining statistical and systematic uncertainties, the final error
should of the order of 1%.
.
Therefore combining statistical and systematic uncertainties, the final error
should of the order of 1%.
Since the value of  of Ref. [2] is
1.5 standard deviation away from zero, it would be significant
to repeat that test with an error of, let us say, 1%. Of course,
this test is not one that can be considered as unique at
a
of Ref. [2] is
1.5 standard deviation away from zero, it would be significant
to repeat that test with an error of, let us say, 1%. Of course,
this test is not one that can be considered as unique at
a  --factory. However it would establish a limit
for spontaneous decoherence in regeneration of kaons comparable to
the limit of 0.6% obtained
for decoherence in neutron interferometry, [6].
--factory. However it would establish a limit
for spontaneous decoherence in regeneration of kaons comparable to
the limit of 0.6% obtained
for decoherence in neutron interferometry, [6].




Next: 3 Two-Kaon Systems.
Up: Chapter 2 Section 1
Previous: 1 Introduction.
Carlos E.Piedrafita


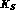 regeneration have been
proposed long ago, [1]. They consist
of transporting a neutral kaon beam over a distance long enough for all
its
regeneration have been
proposed long ago, [1]. They consist
of transporting a neutral kaon beam over a distance long enough for all
its 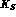 --component to decay; letting it impinge on a piece of material
called regenerator; and recording the number
of decays into two charged pions as a function of distance to that
regenerator.
--component to decay; letting it impinge on a piece of material
called regenerator; and recording the number
of decays into two charged pions as a function of distance to that
regenerator.
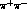 :
:
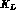 and decay via the CP violating mode;
and decay via the CP violating mode;

 regeneration followed by a CP conserving decay.
regeneration followed by a CP conserving decay.
 can be considered as a pure state
in each momentum interval, if that interval is small enough.
Because the kaon has spin zero,
all configurations of its
can be considered as a pure state
in each momentum interval, if that interval is small enough.
Because the kaon has spin zero,
all configurations of its  --decays
can be considered as two pions in an S--wave state,
which is a pure state.
Thus, at each momentum, the two-pion state
from the decay of a kaon in the very forward direction is
a pure state. Whether the kaon is transmitted or
coherently regenerated, the state of the regenerator is
the same, after as well as before the kaon traversed it.
Therefore the two processes interfere between one another.
As a function of proper time t, the decay rate can be written
as
--decays
can be considered as two pions in an S--wave state,
which is a pure state.
Thus, at each momentum, the two-pion state
from the decay of a kaon in the very forward direction is
a pure state. Whether the kaon is transmitted or
coherently regenerated, the state of the regenerator is
the same, after as well as before the kaon traversed it.
Therefore the two processes interfere between one another.
As a function of proper time t, the decay rate can be written
as
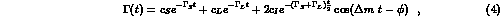
 and
and  are the total decay rates of the
are the total decay rates of the 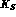 and of the
and of the
 mesons, respectively;
mesons, respectively; 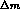 is the
is the  --
--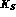 mass difference;
and
mass difference;
and 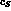 ,
,  ,
, 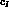 , and
, and  are parameters that
can be measured by the shape of the time distribution
are parameters that
can be measured by the shape of the time distribution 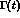 .
.
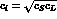 .
In accordance with Eq. (
.
In accordance with Eq. (
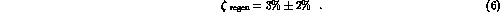
 ne .
The accuracy would be improved.
For instance, one may surround one of the two intersection points
with a regenerator of a cylindric form, with its axis along the
ne .
The accuracy would be improved.
For instance, one may surround one of the two intersection points
with a regenerator of a cylindric form, with its axis along the 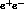 beam
line, with a radius of 20 cm and a height of 20 cm too. The regenerator
would intercept
beam
line, with a radius of 20 cm and a height of 20 cm too. The regenerator
would intercept  emitted within a solid angle of about 5 sr. The
thickness of the cylinder should be adjusted to produce,
just behind the regenerator, more
emitted within a solid angle of about 5 sr. The
thickness of the cylinder should be adjusted to produce,
just behind the regenerator, more  --decays by regenerated
--decays by regenerated 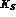 than by transmitted
than by transmitted 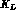 . Then one makes sure that
the
. Then one makes sure that
the 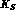 --
--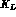 interference pattern visible in the
interference pattern visible in the  --mode is
as long as possible. For instance, a beryllium cylinder 2.4 cm thick
would be an adequate regenerator. It would regenerate one
--mode is
as long as possible. For instance, a beryllium cylinder 2.4 cm thick
would be an adequate regenerator. It would regenerate one  in
10
in
10 according to Ref. [
according to Ref. [ .
.
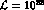 , in one month calendar time with
an efficiency of 30%, i.e. an integrated luminosity of 1000 pb
, in one month calendar time with
an efficiency of 30%, i.e. an integrated luminosity of 1000 pb ,
one may expect more than 10
,
one may expect more than 10
 \
through the regenerator according to Refs. [
\
through the regenerator according to Refs. [ would be measured with
a statistical error of less 1%.
If the angle of the kaon emerging from the regenerator
can be determined to better than 20 mr, the effect of the incoherent
regeneration and elastic scattering should introduce an uncertainty
of less than 1%.
Finally one should to be able to eliminate background
in
would be measured with
a statistical error of less 1%.
If the angle of the kaon emerging from the regenerator
can be determined to better than 20 mr, the effect of the incoherent
regeneration and elastic scattering should introduce an uncertainty
of less than 1%.
Finally one should to be able to eliminate background
in  --decays down to less
than 10
--decays down to less
than 10 times the
times the  decay rate into
decay rate into  \
at a machine like Da
\
at a machine like Da ne \
designed to measure the CP violation parameter
called
ne \
designed to measure the CP violation parameter
called 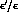 .
Therefore combining statistical and systematic uncertainties, the final error
should of the order of 1%.
.
Therefore combining statistical and systematic uncertainties, the final error
should of the order of 1%.
 of Ref. [
of Ref. [ --factory. However it would establish a limit
for spontaneous decoherence in regeneration of kaons comparable to
the limit of 0.6% obtained
for decoherence in neutron interferometry, [
--factory. However it would establish a limit
for spontaneous decoherence in regeneration of kaons comparable to
the limit of 0.6% obtained
for decoherence in neutron interferometry, [