3.2 Realistic set--up

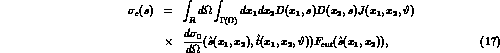
Computing QED corrections over a realistic set--up is a much more involved problem, since the corrections, besides being large, critically depend on the experimental cuts such as energy or invariant mass thresholds, angular acceptance, acollinearity cut and so on. In this case, the structure function approach allows to write the corrected cross section in the laboratory frame in the following form [2,3]:

where the angular integration has to be understood as follows:

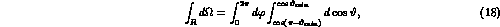
with 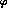and the azimuthal and polar angle of the scattered fermion. Here we limit ourselves to give a general description of eq. (17). For more details and explicit formulae the reader is referred to [2,3]. 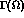stands for the portion of the initial state radiation phase space allowed by realistic cuts; it can be analytically delimited by solving the kinematics of the hard scattering process in the presence of initial state radiation if one assumes soft and/or collinear approximation and hence derives the limits on the variables imposed by realistic cuts. 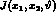is the Jacobian of the transformation from the centre of mass to the laboratory frame and accounts for the boost caused by the emission of unbalanced radiation by the initial state radiation. In the ultrarelativistic approximation its expression reads:

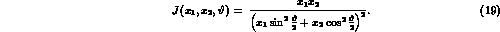
The photonic content of the structure function 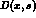can be directly read by its explicit expression [6]:

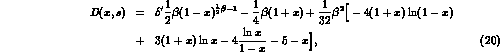
which one obtains by solving, according to well--established techniques [6], the Lipatov -- Altarelli -- Parisi evolution equation satisfied by 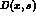in terms of the one--loop expression for the splitting function 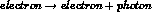. This allows to resum large mass logarithms from soft multiphoton emission and to include hard photon effects up to . In the K-factor one reabsorbs next--to--leading contributions matching the perturbative results for the specific process under consideration.

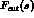provides the final state QED correction to the cross section in the presence of realistic experimental cuts. Its 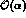analytic expression is known but it is too lengthy to be displayed here and can be found in [9]. It should be emphasized that in a realistic set--up higher order final state corrections could become relevant pointing out the need of introducing a resummation procedure of large logarithms. A detailed discussion about different prescriptions for treating higher order final state effects is given in [2,3]. Moreover, when considering final state corrections to Bhabha scattering, one is also faced with the problem of the calorimetric measurement for electrons since what is detected is an electromagnetic jet of semi--aperture , where is an experimental parameter describing the resolution power of the calorimeter. In our approach this effect is accounted for by adding to the 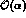part of the final state QED correction the contribution due to the emission of an hard photon with an energy fraction greater than 1-x, where x is for an invariant mass cut and 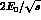for an energy threshold cut, and collinear with the final fermion within an angle 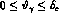. For high--energy electrons the contribution reads [10]

where

Eq. (21) is valid in the approximation 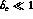rad and 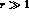which is safely satisfied at DANE energies.

The master formula (17) needs further manipulations in order to extract numerically stable and fast predictions. Indeed this expression as it stands exhibits several computational problems which can be solved by an appropriate regularization procedure, described in detail in [3], namely the variance--reducing technique known as ``control variates''. Then the corrected cross section can be written as the the sum of an analytical term, of a one--dimensional integral in the radiator form (containing the bulk of the whole contribution) and terms with one--, two-- and three--dimensional integrals controlling the angular and acollinearity effects which, albeit important, are generally a small contribution as compared with the effect due to an invariant mass cut alone. The above regularization procedure is implemented in the FORTRAN program for electroweak physics at LEP/SLC energies TOPAZ0 [11].

A few comments are in order here about the accuracy of the theoretical predictions derivable from eq. (17) for resonant and non resonant hard scattering processes measured over a realistic set--up. Actually, it should be noted that, whereas any 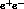large angle process (including Bhabha scattering) at LEP/SLC energies is a resonant process with small non--resonant contributions, this is not the case of leptonic production at DANE. As a consequence, non leading contributions not included in our approach (initial state hard photon constant terms and initial--final state interference) are almost negligible (of order, say, few 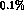) only for the case of the line--shape where the above effects are strongly suppressed by the very narrow width of the resonance. This argument obviously does not apply to non--resonant processes at DANE and therefore the theoretical error, depending on the cuts, becomes larger (presumably of order of a few per cent) and the predictions have to be understood (especially for Bhabha scattering) as leading log ones.

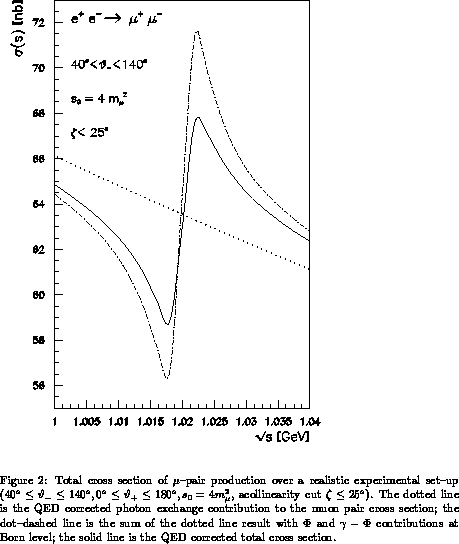
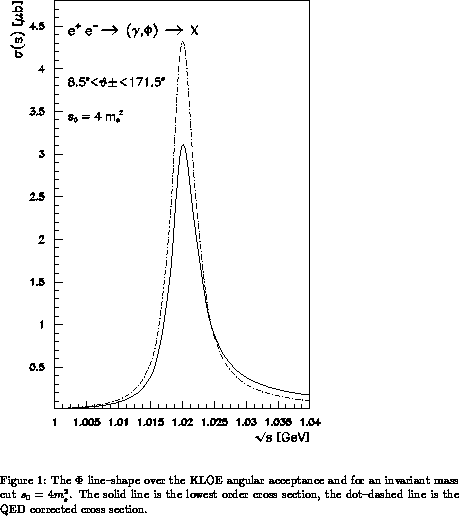
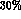Illustrative numerical results are given in Fig. 1 ( line--shape) and Fig. 2 (muon pair cross section) obtained by fitting the program TOPAZ0 to DANE processes. Fig. 1 shows the lowering of the peak cross section (of order ) essentially due soft multiphoton emission and the radiative tail above the peak as a typical convolution hard photon effect. Fig. 2 shows the effects of the QED radiative corrections on the cross section for muon pair production when a realistic experimental set--up is considered.