The treatment of photonic corrections is particularly simple
when no realistic cut is imposed in data taking
-- but an invariant mass one --
and therefore the
experimental analysis is limited to the so--called
extrapolated observables.
Actually, for such a configuration,
one of the two integrations over the radiative
variables 
and 
in eq. (9) can be analytically performed
and the initial state corrected
cross section is given by the following
one--dimensional convolution formula [5,6]:
where
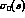is the total Born cross section
of the specific hard scattering process under consideration.
The parameter 
is defined by:
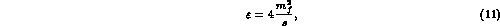
when including the whole photon phase space and can be used
to account for a cut on the invariant mass
after initial state radiation 
by replacing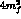 
with the cut 
.
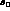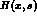is known as the radiator
and it gives the probability that a fraction
x of the center of mass energy s is carried away
by initial state radiation
(up to some photon energy resolution
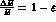). The radiator is
a universal (process independent) quantity linked to the
structure functions by the relation:
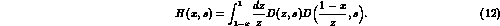
Its explicit expression reads as follows [6]:
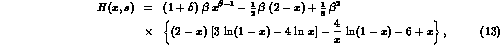
with
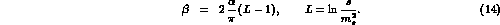
The first exponentiated term takes into account
soft multiphoton emission and the second and third terms describe
hard bremsstrahlung up to 
. The factor 
reabsorbs next--to--leading (process dependent) corrections not
kept under control
by the approach which can be however included
by relying upon explicit perturbative calculations. For instance, for
a pure s-channel resonant cross section, 
is given by
the following 
factor:
where 
is the Riemann function. The K- factor (15) comes
from
the infrared cancellation between the two--loop electron form factor and
soft double bremsstrahlung. In the limit of small photon energy
resolution, eq. (10), which is currently used by
the LEP collaborations
to analyze the so--called perfect data of LEP 1 processes,
reduces to the results of the
coherent state approach [8] in terms of infrared factors to all orders
and finite order next--to--leading corrections.
For the extrapolated set--up,
final state radiation can be easily included by multiplying
the kernel cross section by a factor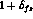 
obtained
by computing the exact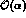 
matrix element for
s--channel 
(where the photon is
emitted by the final state only) and integrating it over the phase space
allowed by cuts [9].
If we assume that only an invariant mass cut such as
is present, the following correction factor has
to be included:
where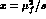 
. When no cuts at all are applied, 
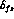reduces to the well--known and very small 
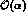factor
.
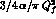