


Next: Acknowledgments
Up: Chapter 10 Section 8
Previous: 3.2 Realistic set--up
In the context of the experiments at the  --factory
an accurate knowledge of the radiative Bhabha scattering
cross section is mandatory
because the process constitutes the main background for
--factory
an accurate knowledge of the radiative Bhabha scattering
cross section is mandatory
because the process constitutes the main background for
 physics experiments with
tagging facilities [12,13].
Theoretical predictions are required for
various experimental configurations which include an extremely very forward
angular set--up, as can be seen from the following list:
physics experiments with
tagging facilities [12,13].
Theoretical predictions are required for
various experimental configurations which include an extremely very forward
angular set--up, as can be seen from the following list:
- the cross section in the region
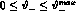 ,
, 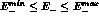 , with
, with
 few mrad,
few mrad, 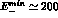 MeV and
MeV and
 MeV, both totally inclusive on the positron and
the photon and with acceptance cuts on them
(this includes: single tagging rates
for small angle scattered electron (SAST),
double tagging rates for both electron and positron at small angle (SADT),
coincidence rate of electron and photon in the forward direction (SAEPC));
MeV, both totally inclusive on the positron and
the photon and with acceptance cuts on them
(this includes: single tagging rates
for small angle scattered electron (SAST),
double tagging rates for both electron and positron at small angle (SADT),
coincidence rate of electron and photon in the forward direction (SAEPC));
- the cross section for the light spot (LS), i.e. photons detected in
the forward direction with energy
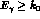 , with
, with 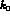 of order
few MeV;
of order
few MeV;
- the cross section for the electron in the small angle
region defined above and the positron at
large angle (SLDT), in particular in the
region covered by the detector KLOE [14]
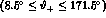 ;
;
- the cross section for both electron and positron at large angle
(
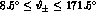 ),
but accompanied by
a photon of energy
),
but accompanied by
a photon of energy 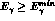 at a minimum angle
at a minimum angle
 from any of the final state fermions (LLDT).
from any of the final state fermions (LLDT).
Although analytic results for differential and total cross sections of
 are available in the literature
(refs. [15]--[17] is an indicative list of such calculations),
a detailed analysis of all single and double tagging configurations
demands an exact evaluation of the matrix element in
the very forward direction, where the momentum transfer is of order
are available in the literature
(refs. [15]--[17] is an indicative list of such calculations),
a detailed analysis of all single and double tagging configurations
demands an exact evaluation of the matrix element in
the very forward direction, where the momentum transfer is of order  and the
and the 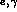 scattering angles
scattering angles 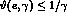 ,
with
,
with 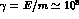 at DA
at DA NE.
NE.
Unfortunately, in these extreme kinematical conditions the
squared matrix element of ref. [18], with the finite mass corrections
obviously included, is inapplicable, namely it leads to an unphysical
negative result for hard photon
emission collinear to the very forward electron direction. Indeed, as discussed
in [19], the CALKUL collaboration's result [18]
is valid only in the limit  whereas in the very forward direction the minimum four--momentum
exchange
whereas in the very forward direction the minimum four--momentum
exchange 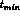 is given by:
is given by:
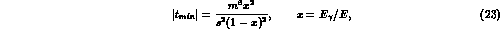
up to 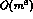 . Moreover,
as a consequence of the approximation used in ref. [18],
``off--diagonal'' terms of the form
. Moreover,
as a consequence of the approximation used in ref. [18],
``off--diagonal'' terms of the form
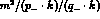 ,
associated to initial--final state interference, are missing. However,
for very small electron scattering angles they become of the same order of
``diagonal'' terms
,
associated to initial--final state interference, are missing. However,
for very small electron scattering angles they become of the same order of
``diagonal'' terms
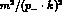 or
or 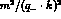 describing initial and final state radiation respectively.
This is due to the fact that in the very forward region initial
and final radiation cones overlap and interfere and therefore
the contribution of ``off--diagonal'' mass
terms become more and more important when the electron scattering angle goes to
zero.
describing initial and final state radiation respectively.
This is due to the fact that in the very forward region initial
and final radiation cones overlap and interfere and therefore
the contribution of ``off--diagonal'' mass
terms become more and more important when the electron scattering angle goes to
zero.
For the above reasons, we computed by using SCHOONSCHIP [20]
the complete squared matrix element
of the (gauge invariant) t--channel diagrams associated
with electron radiation. Positron radiation and electron and positron
interference can be safely neglected being suppressed by the
stringent constraints on the electron energy.
Then the full expression for the
squared matrix element, including all
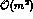 ,
, 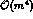 and
and 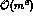 terms,
reads as follows [19]:
terms,
reads as follows [19]:

where
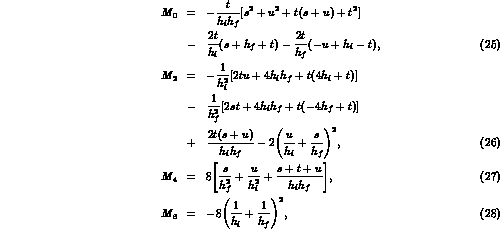
with  ,
, 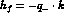 . The other invariants
are defined as follows:
. The other invariants
are defined as follows:
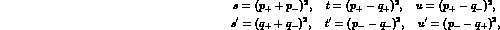
where 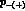 and
and  are the four--momenta of the incoming and
outgoing electron (positron). The squared
matrix element (24) coincides
with the result obtained independently in [21].
are the four--momenta of the incoming and
outgoing electron (positron). The squared
matrix element (24) coincides
with the result obtained independently in [21].
Based on the analytic result (24), the
semi--analytical program
PHIPHI [22] has been developed in order to obtain
phenomenological predictions of interest at DA NE. Some results are
shown in Fig. 3 -- 5 together with comparisons with those
existing in the literature.
NE. Some results are
shown in Fig. 3 -- 5 together with comparisons with those
existing in the literature.
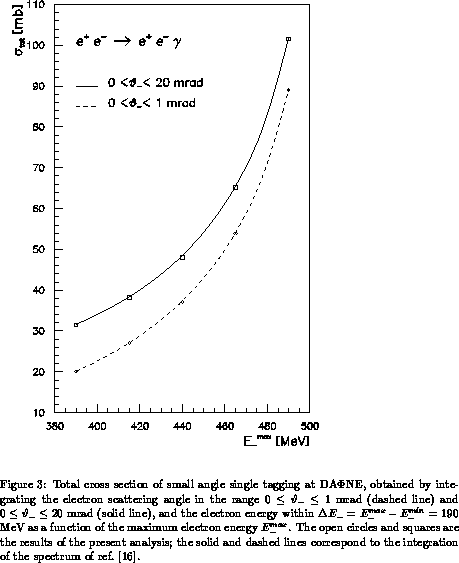
In Fig. 3 the total cross section of small angle single
tagging at DA NE obtained by integrating the electron
energy over the range
NE obtained by integrating the electron
energy over the range 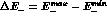 = 190 MeV is shown
as a function of the
maximum electron energy
= 190 MeV is shown
as a function of the
maximum electron energy  . The solid and dashed lines
correspond to the integration of
the spectrum
. The solid and dashed lines
correspond to the integration of
the spectrum 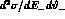 of ref. [16]
in two different domains of the electron scattering angle,
namely
of ref. [16]
in two different domains of the electron scattering angle,
namely 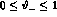 mrad (dashed line) and
mrad (dashed line) and
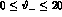 mrad (solid line). Our results
are represented by the open circles
and squares showing a fully satisfactory agreement
with the integration of the analytical result of [16]. For the energy
and angle intervals of interest at DA
mrad (solid line). Our results
are represented by the open circles
and squares showing a fully satisfactory agreement
with the integration of the analytical result of [16]. For the energy
and angle intervals of interest at DA NE, i.e.
NE, i.e.
 MeV and
MeV and
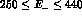 MeV with
MeV with 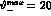 mrad the total cross
section is about 35, 50 mb respectively.
mrad the total cross
section is about 35, 50 mb respectively.
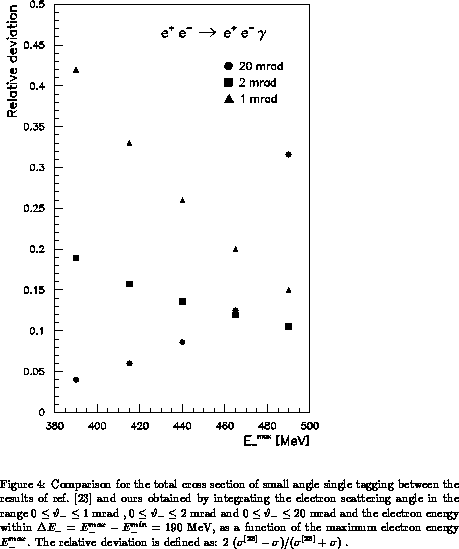
Fig. 4 shows a comparison for the
total cross section of SAST between the recent results
of ref. [23] and ours obtained with
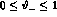 mrad ,
mrad ,  mrad and
mrad and
 mrad and the electron energy within
mrad and the electron energy within
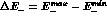 = 190 MeV,
as a function of the maximum electron
energy
= 190 MeV,
as a function of the maximum electron
energy  . More in detail, in ref. [23] an approximate formula
for the total cross section of SAST in the forward region,
with a radiative energy loss of at least
. More in detail, in ref. [23] an approximate formula
for the total cross section of SAST in the forward region,
with a radiative energy loss of at least 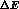 and momentum
transfer in the range
and momentum
transfer in the range 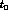 and
and 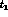 , is given as:
, is given as:

with
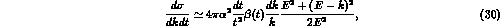
and the function
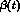 takes the form:
takes the form:
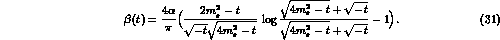
As can be seen by Fig. 4, the approximate
result derived in [23] provides a good estimate of the SAST
cross section with an accuracy of order 5--10 % when the kinematical
configuration proposed
in ref. [13] ( mrad,
250 MeV
mrad,
250 MeV 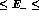 440 MeV) is assumed. In the limit of small
electron scattering angles (
440 MeV) is assumed. In the limit of small
electron scattering angles ( mrad) the relative deviation
decreases as
mrad) the relative deviation
decreases as  increases, consistently with the soft, collinear and
no--recoil approximation adopted in ref. [23].
increases, consistently with the soft, collinear and
no--recoil approximation adopted in ref. [23].
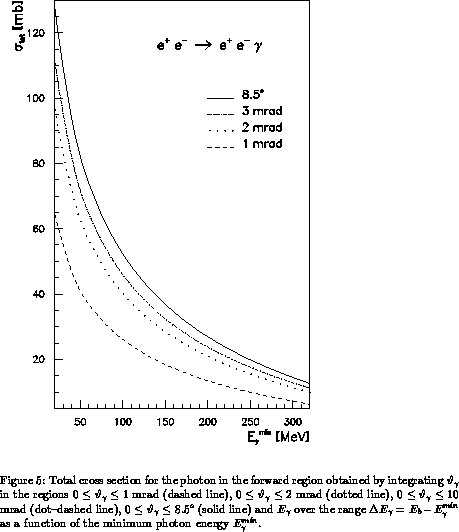
The total cross section for photons emitted in the forward
region is shown in Fig. 5. The results are obtained by integrating the photon
energy 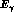 over the range
over the range
 as a function of the
minimum photon energy
as a function of the
minimum photon energy 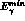 .
The different curves correspond to
.
The different curves correspond to 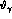 in the regions
in the regions  mrad
(dashed line),
mrad
(dashed line), 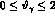 mrad (dotted line),
mrad (dotted line),
 mrad (dash--dotted line),
mrad (dash--dotted line),
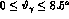 (solid line). The physical
content of Fig. 5 is that the radiation is essentially emitted
within a cone of half--opening angle of 2 mrad, as expected from the
collinear nature of the bremsstrahlung mechanism.
(solid line). The physical
content of Fig. 5 is that the radiation is essentially emitted
within a cone of half--opening angle of 2 mrad, as expected from the
collinear nature of the bremsstrahlung mechanism.
Further numerical results for the total cross section of small angle
electron--photon double tagging, of small--large and large--large
electron--positron double tagging can be found in [19].
Our results, obtained by the code PHIPHI,
has been checked very recently by the Monte Carlo generator
BBBREM [24] and found in very good agreement [25].
In particular, for the unconstrained
kinematics, we also agree with the single photon spectrum and
the total cross section derived in refs. [15,16].
We would like to point out, in conclusion, that
for the SLDT case, where for kinematical reasons
no mass divergences appear, the ultrarelativistic matrix element
of ref. [18] can
be safely used. In the LLDT case mass divergences do appear but the condition
 is fulfilled so that complete CALKUL result
do apply. In all the other cases
(SAST, SADT, SAEPC and LS) one has both mass divergences and very small angles,
so that the full matrix element of eq. (24), including quartic and
sextic mass correction terms, must be used.
is fulfilled so that complete CALKUL result
do apply. In all the other cases
(SAST, SADT, SAEPC and LS) one has both mass divergences and very small angles,
so that the full matrix element of eq. (24), including quartic and
sextic mass correction terms, must be used.



Next: Acknowledgments
Up: Chapter 10 Section 8
Previous: 3.2 Realistic set--up
Carlos E.Piedrafita
 --factory
an accurate knowledge of the radiative Bhabha scattering
cross section is mandatory
because the process constitutes the main background for
--factory
an accurate knowledge of the radiative Bhabha scattering
cross section is mandatory
because the process constitutes the main background for
 physics experiments with
tagging facilities [12,13].
Theoretical predictions are required for
various experimental configurations which include an extremely very forward
angular set--up, as can be seen from the following list:
physics experiments with
tagging facilities [12,13].
Theoretical predictions are required for
various experimental configurations which include an extremely very forward
angular set--up, as can be seen from the following list:
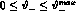 ,
, 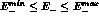 , with
, with
 few mrad,
few mrad, 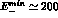 MeV and
MeV and
 MeV, both totally inclusive on the positron and
the photon and with acceptance cuts on them
(this includes: single tagging rates
for small angle scattered electron (SAST),
double tagging rates for both electron and positron at small angle (SADT),
coincidence rate of electron and photon in the forward direction (SAEPC));
MeV, both totally inclusive on the positron and
the photon and with acceptance cuts on them
(this includes: single tagging rates
for small angle scattered electron (SAST),
double tagging rates for both electron and positron at small angle (SADT),
coincidence rate of electron and photon in the forward direction (SAEPC));
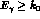 , with
, with 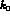 of order
few MeV;
of order
few MeV;
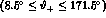 ;
;
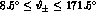 ),
but accompanied by
a photon of energy
),
but accompanied by
a photon of energy 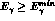 at a minimum angle
at a minimum angle
 from any of the final state fermions (LLDT).
from any of the final state fermions (LLDT).

 are available in the literature
(refs. [
are available in the literature
(refs. [ and the
and the 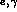 scattering angles
scattering angles 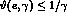 ,
with
,
with 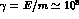 at DA
at DA NE.
NE.
 whereas in the very forward direction the minimum four--momentum
exchange
whereas in the very forward direction the minimum four--momentum
exchange 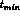 is given by:
is given by:
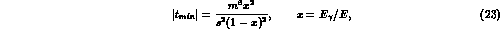
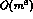 . Moreover,
as a consequence of the approximation used in ref. [
. Moreover,
as a consequence of the approximation used in ref. [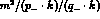 ,
associated to initial--final state interference, are missing. However,
for very small electron scattering angles they become of the same order of
``diagonal'' terms
,
associated to initial--final state interference, are missing. However,
for very small electron scattering angles they become of the same order of
``diagonal'' terms
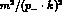 or
or 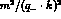 describing initial and final state radiation respectively.
This is due to the fact that in the very forward region initial
and final radiation cones overlap and interfere and therefore
the contribution of ``off--diagonal'' mass
terms become more and more important when the electron scattering angle goes to
zero.
describing initial and final state radiation respectively.
This is due to the fact that in the very forward region initial
and final radiation cones overlap and interfere and therefore
the contribution of ``off--diagonal'' mass
terms become more and more important when the electron scattering angle goes to
zero.
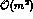 ,
, 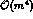 and
and 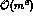 terms,
reads as follows [
terms,
reads as follows [
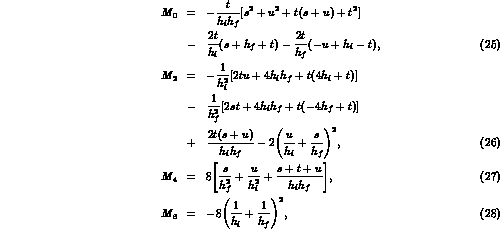
 ,
, 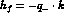 . The other invariants
are defined as follows:
. The other invariants
are defined as follows:
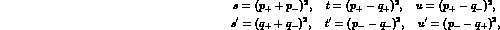
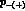 and
and  are the four--momenta of the incoming and
outgoing electron (positron). The squared
matrix element (
are the four--momenta of the incoming and
outgoing electron (positron). The squared
matrix element ( NE. Some results are
shown in Fig. 3 -- 5 together with comparisons with those
existing in the literature.
NE. Some results are
shown in Fig. 3 -- 5 together with comparisons with those
existing in the literature.
 NE obtained by integrating the electron
energy over the range
NE obtained by integrating the electron
energy over the range 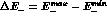 = 190 MeV is shown
as a function of the
maximum electron energy
= 190 MeV is shown
as a function of the
maximum electron energy  . The solid and dashed lines
correspond to the integration of
the spectrum
. The solid and dashed lines
correspond to the integration of
the spectrum 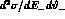 of ref. [
of ref. [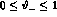 mrad (dashed line) and
mrad (dashed line) and
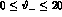 mrad (solid line). Our results
are represented by the open circles
and squares showing a fully satisfactory agreement
with the integration of the analytical result of [
mrad (solid line). Our results
are represented by the open circles
and squares showing a fully satisfactory agreement
with the integration of the analytical result of [ NE, i.e.
NE, i.e.
 MeV and
MeV and
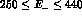 MeV with
MeV with 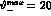 mrad the total cross
section is about 35, 50 mb respectively.
mrad the total cross
section is about 35, 50 mb respectively.

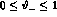 mrad ,
mrad ,  mrad and
mrad and
 mrad and the electron energy within
mrad and the electron energy within
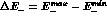 = 190 MeV,
as a function of the maximum electron
energy
= 190 MeV,
as a function of the maximum electron
energy  . More in detail, in ref. [
. More in detail, in ref. [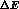 and momentum
transfer in the range
and momentum
transfer in the range 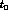 and
and 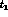 , is given as:
, is given as:

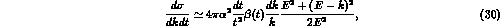
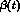 takes the form:
takes the form:
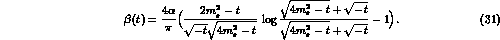
 mrad,
250 MeV
mrad,
250 MeV 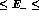 440 MeV) is assumed. In the limit of small
electron scattering angles (
440 MeV) is assumed. In the limit of small
electron scattering angles ( mrad) the relative deviation
decreases as
mrad) the relative deviation
decreases as  increases, consistently with the soft, collinear and
no--recoil approximation adopted in ref. [
increases, consistently with the soft, collinear and
no--recoil approximation adopted in ref. [
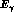 over the range
over the range
 as a function of the
minimum photon energy
as a function of the
minimum photon energy 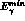 .
The different curves correspond to
.
The different curves correspond to 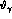 in the regions
in the regions  mrad
(dashed line),
mrad
(dashed line), 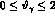 mrad (dotted line),
mrad (dotted line),
 mrad (dash--dotted line),
mrad (dash--dotted line),
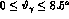 (solid line). The physical
content of Fig. 5 is that the radiation is essentially emitted
within a cone of half--opening angle of 2 mrad, as expected from the
collinear nature of the bremsstrahlung mechanism.
(solid line). The physical
content of Fig. 5 is that the radiation is essentially emitted
within a cone of half--opening angle of 2 mrad, as expected from the
collinear nature of the bremsstrahlung mechanism.
 is fulfilled so that complete CALKUL result
do apply. In all the other cases
(SAST, SADT, SAEPC and LS) one has both mass divergences and very small angles,
so that the full matrix element of eq. (
is fulfilled so that complete CALKUL result
do apply. In all the other cases
(SAST, SADT, SAEPC and LS) one has both mass divergences and very small angles,
so that the full matrix element of eq. (