



Next: 3.1 Predictions and Errors.
Up: Chapter 2 Section 1
Previous: 2 Test Performed in
The really unique tests of quantum mechanics at Da ne are
tests with quantum states made of two kaons.
In
ne are
tests with quantum states made of two kaons.
In  --collisions of this kind of energy, only objects odd
under charge conjugation are formed. The two-neutral-kaon system
created via
--collisions of this kind of energy, only objects odd
under charge conjugation are formed. The two-neutral-kaon system
created via  production and two-body decay in a given direction is
in a pure quantum state. Its state vector can be expressed as
production and two-body decay in a given direction is
in a pure quantum state. Its state vector can be expressed as
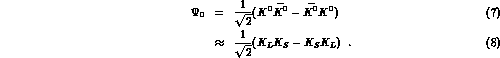
In the terms 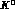
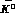 ,
, 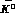
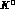 ,
, 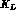
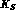 , and
, and 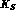
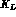 , the first symbol
refers to the state of the particle emitted on the left and the second
symbol to the particle on the right. The sign
, the first symbol
refers to the state of the particle emitted on the left and the second
symbol to the particle on the right. The sign  is used in
Eq. (8) instead of the sign = because of a slight inaccuracy in the
normalization factor.
is used in
Eq. (8) instead of the sign = because of a slight inaccuracy in the
normalization factor.
As stated above, kaons living long enough to be reduced
to their  component
are pure states and
component
are pure states and 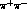 --decay states are equivalent to
pure
--decay states are equivalent to
pure 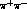 S--wave states. If we accept the
S--wave states. If we accept the 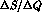 rule,
each of the semileptonic decay states
rule,
each of the semileptonic decay states  \
and
\
and  can also be considered as a pure state in the context of
this paper. As to multiple-particle states where the kaon
on the left has decayed into a pure state
can also be considered as a pure state in the context of
this paper. As to multiple-particle states where the kaon
on the left has decayed into a pure state 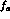 and the kaon on the right
into a pure state
and the kaon on the right
into a pure state 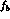 , they are pure states themselves.
All processes leading from
the initial
, they are pure states themselves.
All processes leading from
the initial  --meson to any one of these pure
multiparticle final states
--meson to any one of these pure
multiparticle final states 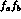 interfere between each other.
interfere between each other.
In particular, consider the possibility of having the same decay state f,
for instance 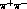 , or
, or 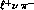 , or
, or 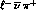 , as the final decay product
on the left as well as on the right.
This may happen via two processes,
, as the final decay product
on the left as well as on the right.
This may happen via two processes,
1) a 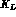 emitted to the left and a
emitted to the left and a  to the right; or
to the right; or
2) a 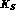 to the left and a
to the left and a  to the right;
to the right;
and, in either case, both the 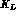 and the
and the 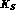 decaying into the
same state f. These two processes interfere between one another.
decaying into the
same state f. These two processes interfere between one another.
Let 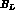 and
and 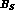 be the branching ratios of
be the branching ratios of 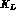 and
and  ,
respectively, into the decay state f .
From Eq. (8), one gets the probability for the kaon
on the left to decay into f at the proper time
,
respectively, into the decay state f .
From Eq. (8), one gets the probability for the kaon
on the left to decay into f at the proper time  and
the one on the right to decay into f at proper time
and
the one on the right to decay into f at proper time  ,
per unit of
,
per unit of 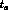 and unit of
and unit of 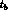 :
:

The third term in the largest bracket of Eq. (9)
is the interference term.
For  , that term is negative and large enough to
make
, that term is negative and large enough to
make  .
However, if, for any reason, the interference term is reduced by
a factor
.
However, if, for any reason, the interference term is reduced by
a factor 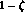 , the rate for
, the rate for 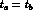 becomes non-zero.
These conditions are particularly favorable for a test of quantum mechanics
because, then, the test for
becomes non-zero.
These conditions are particularly favorable for a test of quantum mechanics
because, then, the test for  is a null experiment.
is a null experiment.




Next: 3.1 Predictions and Errors.
Up: Chapter 2 Section 1
Previous: 2 Test Performed in
Carlos E.Piedrafita
 ne are
tests with quantum states made of two kaons.
In
ne are
tests with quantum states made of two kaons.
In  --collisions of this kind of energy, only objects odd
under charge conjugation are formed. The two-neutral-kaon system
created via
--collisions of this kind of energy, only objects odd
under charge conjugation are formed. The two-neutral-kaon system
created via  production and two-body decay in a given direction is
in a pure quantum state. Its state vector can be expressed as
production and two-body decay in a given direction is
in a pure quantum state. Its state vector can be expressed as
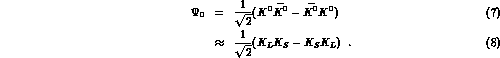
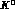
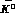 ,
, 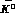
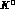 ,
, 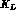
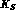 , and
, and 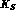
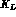 , the first symbol
refers to the state of the particle emitted on the left and the second
symbol to the particle on the right. The sign
, the first symbol
refers to the state of the particle emitted on the left and the second
symbol to the particle on the right. The sign  is used in
Eq. (
is used in
Eq. ( component
are pure states and
component
are pure states and 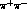 --decay states are equivalent to
pure
--decay states are equivalent to
pure 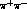 S--wave states. If we accept the
S--wave states. If we accept the 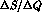 rule,
each of the semileptonic decay states
rule,
each of the semileptonic decay states  \
and
\
and  can also be considered as a pure state in the context of
this paper. As to multiple-particle states where the kaon
on the left has decayed into a pure state
can also be considered as a pure state in the context of
this paper. As to multiple-particle states where the kaon
on the left has decayed into a pure state 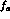 and the kaon on the right
into a pure state
and the kaon on the right
into a pure state 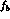 , they are pure states themselves.
All processes leading from
the initial
, they are pure states themselves.
All processes leading from
the initial  --meson to any one of these pure
multiparticle final states
--meson to any one of these pure
multiparticle final states 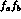 interfere between each other.
interfere between each other.
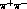 , or
, or 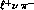 , or
, or 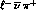 , as the final decay product
on the left as well as on the right.
This may happen via two processes,
, as the final decay product
on the left as well as on the right.
This may happen via two processes, 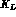 emitted to the left and a
emitted to the left and a  to the right; or
to the right; or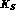 to the left and a
to the left and a  to the right;
to the right;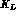 and the
and the 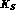 decaying into the
same state f. These two processes interfere between one another.
decaying into the
same state f. These two processes interfere between one another.
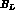 and
and 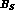 be the branching ratios of
be the branching ratios of 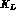 and
and  ,
respectively, into the decay state f .
From Eq. (
,
respectively, into the decay state f .
From Eq. ( and
the one on the right to decay into f at proper time
and
the one on the right to decay into f at proper time  ,
per unit of
,
per unit of 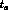 and unit of
and unit of 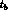 :
:

 , that term is negative and large enough to
make
, that term is negative and large enough to
make  .
However, if, for any reason, the interference term is reduced by
a factor
.
However, if, for any reason, the interference term is reduced by
a factor 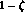 , the rate for
, the rate for 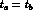 becomes non-zero.
These conditions are particularly favorable for a test of quantum mechanics
because, then, the test for
becomes non-zero.
These conditions are particularly favorable for a test of quantum mechanics
because, then, the test for  is a null experiment.
is a null experiment.