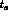 and
and  measured in units of the
measured in units of the  average lifetime,
average lifetime,
Let us use the variable z, which we define in each event
as the difference between 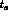 and
and  measured in units of the
measured in units of the  average lifetime,
average lifetime,

Considering those events where
both kaons of the pair decay via the same
decay mode, one can integrate all those with the same  ,
(i.e. with the same z) over the
variable
,
(i.e. with the same z) over the
variable  and histogram them
as a function of the variable z. In each bin of width dz,
the number of events
and histogram them
as a function of the variable z. In each bin of width dz,
the number of events 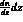 is a function of z that can be developed up to second order in z
around the point z=0. Because of the symmetry between the kaon on the left
and the kaon on the right, the term in z to the first power is zero.
is a function of z that can be developed up to second order in z
around the point z=0. Because of the symmetry between the kaon on the left
and the kaon on the right, the term in z to the first power is zero.
 and
and  are two parameters that can be obtained from a fit to the data.
are two parameters that can be obtained from a fit to the data.
Let N be the number of pairs emitted in the fiducial volume,  and
and  the
the 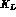 - and the
- and the  -branching ratios,
-branching ratios,  and
and  the
the  - and the
- and the
 -decay rates, as above. Let us define the constants A and
-decay rates, as above. Let us define the constants A and  :
:
using Ref. [7]. In absence of background, quantum mechanics predicts
If there is background and if, because of a possible violation
of quantum mechanics, the interference term is reduced by a factor  ,
,
Measuring  permits us to determine the decoherence parameter
permits us to determine the decoherence parameter
At the limit of large N, the particular form of Eq. (11) permits us
to derive special expressions for the error  on
on 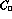 :
:
The proper form to be used
depends on the size of  . The appropriate formula
is always the one that gives the largest error. In any case, the error
. The appropriate formula
is always the one that gives the largest error. In any case, the error 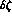 on
on  is given by
is given by
Among the possible sources of background, special attention will be paid
to 

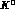
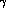 events misidentified as two-body
events misidentified as two-body 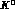
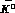 's,
because there are predictions for this effect, [8].
In these background events, the
's,
because there are predictions for this effect, [8].
In these background events, the 
 system is CP=+,
system is CP=+,

and both kaons can decay into the same mode for  .
We call
.
We call  the ratio of the number of these background events to the
number of genuine
the ratio of the number of these background events to the
number of genuine 
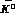 events and, in the numerical applications,
we use the worst (highest) estimate given in
the conclusion of Ref. [8]:
events and, in the numerical applications,
we use the worst (highest) estimate given in
the conclusion of Ref. [8]:  .
Because of the particular dependance
of that background as a function of
.
Because of the particular dependance
of that background as a function of  , we assume that
, we assume that
 can be measured to better than 10% of 2 10
can be measured to better than 10% of 2 10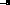 .
.