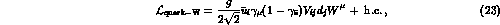
In the Standard Model, the basic quark charged-current interactions are described by the Lagrangian
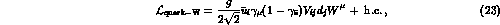
where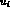 
are the charged 2/3 quarks (
), 
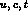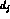the charged 
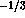quarks (
) and g is the
weak coupling constant (
,
where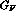 
is the Fermi constant).
V is the
unitary CKM matrix [16]. A useful parametrization is [17,18]
In eq. (24), 
, 
and 
are quark mixing angles
(in particular, 
corresponds approximately to the Cabibbo angle);
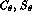, etc., mean
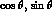, etc.; 
is
the CP-violating phase. Experimental determinations of 
,
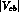and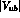 
from K and B decays show that
there is a hierarchy in the mixing angles, so that the CKM matrix can be
empirically
expanded in powers of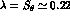 
[19].
Up to and including terms of order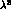 
(
)
for the real (imaginary) part, V is given by
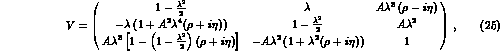
where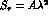 
and
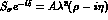. In this particular
(quark) phase convention, the imaginary part of the matrix appears
at order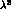 
.
The unitarity of the CKM matrix implies
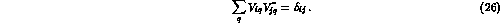
In particular, considering the condition
in the approximation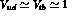 
, one obtains
This relation identifies a triangle in the 
--
plane
(see fig. 1).
The angles of this triangle, 
, 
and 
,
are measures of CP-violation.
Recent phenomenological analyses of the CKM matrix elements can be found in refs. [9,20,21]. A brief discussion of these analyses together with the numerical results, can be found in section 8.
Figure: The unitarity triangle in the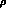 
--
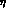plane.
