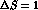Weak decays of light hadrons are more conveniently studied using the Wilson
operator
product expansion (OPE) [22]. With the OPE, it is possible to introduce an
effective Hamiltonian, written in terms of renormalized local operators and of the
corresponding Wilson coefficients [23]--[26].
Short-distance strong-interaction effects
are contained in the coefficients and can be computed in perturbation theory, because of
asymptotic freedom. Long-distance strong-interaction effects are included in the hadronic
matrix elements of the local operators and must be evaluated with some
non-perturbative technique (lattice, QCD sum rules, etc.). The
convenience of the
effective Hamiltonian approach is that all
known non-perturbative methods are usually
able to predict matrix elements of local operators only.
In this section we introduce
the bare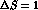 
effective Hamiltonian, the renormalization of which
will be discussed in the next section.
At second order in the weak coupling constant and at zero order in the
strong coupling constant, the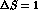 
effective Hamiltonian can be written in terms
of a local product of two charged currents
where 
;
and 
are colour indices
and the sum over repeated indices is understood.
We have introduced the notation
for q=u,c,t.
In terms of the 
, the unitarity condition
of the CKM matrix can be written as
Equation (29)
has been obtained from the original theory, by neglecting all
masses and momenta
with respect to 
.
In practice, the effective Hamiltonian
is obtained by taking 
in the T-product of the two charged currents
and by putting the u, d and s masses to zero.
In order to discuss CP-violation, it is convenient to
write 
as
where 
contains the CP-violating phase and
