In this section, we introduce the parameters
and 
that describe CP-violation in the neutral kaon-system.
In the following, we assume CPT symmetry. A comprehensive
discussion of the general case, including CPT-violation, can be
found in ref. [15].
There are two possible sources of CP-violation in the decays of the
neutral kaons into two pions. CP-violation can take place
both in the kaon mixing matrix and at the decay vertices.
Let us consider the mixing first.
The most general CPT-conserving Hamiltonian of the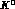 
--
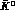system
at rest can be written as
where the bra (ket) can be represented as the two component vector
, 
,
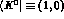M is the ``mass'' matrix and 
is the ``width'' matrix.
Both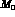 
and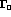 
are real.
Notice that there is some freedom in the definition of the phases of the kaon field. In particular, one can make the change
Correspondingly, the off--diagonal matrix elements of any operator X,
acting on the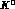 
--
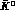system, undergo the changes
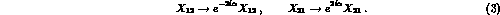
This arbitrariness enters in some popular definitions of the CP-violation parameters. For definiteness, we choose a particular phase convention, namely we require that the CP operator is given by
In this case,
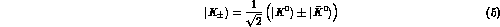
are the CP eigenstates.
In the presence of CP-violation,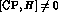 
and the
eigenstates of the Hamiltonian H
are not CP eigenstates.
We introduce the parameter 
which defines the
eigenstates of H as
The corresponding (complex) eigenvalues are denoted as
In the phase convention (4), the parameter 
controls the amount of CP-violation, namely the CP symmetric limit is recovered
for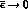 
. We can explicitly write 
in terms of the matrix elements of H
where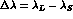 
.
Experimentally CP-violation is a small effect,
i.e. 
. For this reason, one
can simplify eq. (8) to obtain
with
Moreover, since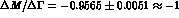 
,
eq. (9)
becomes
In view of the following discussion of the CP-violation parameters, let us introduce amplitudes of the weak decays of kaons into two pions states with definite isospin
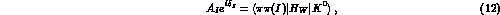
where I=0,2 is the isospin of the final two-pion state and
the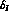 
's are the strong phases induced by final-state interaction.
Watson's theorem ensures that
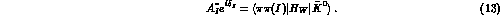
Direct CP-violation, occurring at the decay vertices,
appears as a difference between the amplitudes
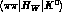and
.
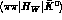This corresponds to a phase difference between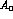 
and
.
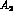One introduces the parameter 
to account for direct CP-violation.
A convenient definition is
where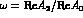 
.
Equation (14) is obtained in
the approximation
,
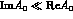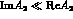and also 
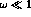, as a consequence of the 
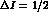enhancement in kaon decays; 
is independent of the kaon phase
convention.
On the contrary,
the parameter 
, defined in eq. (6),
depends on the choice of the phase.
Under a redefinition of the phases as in eq. (2),
changes as
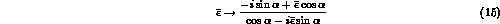
and the CP-symmetric limit does not correspond to
.
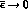
Another parameter, which is independent of the
phase convention and accounts for CP-violation in the mixing
matrix, can be defined in terms of the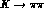 
transition amplitudes
where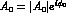 
and the last expression
is obtained in the approximation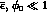 
.
The two definitions, eqs. (6) and (16),
coincide in the Wu-Yang phase convention,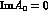 
.
One can check that 
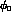changes with the phase convention as
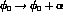and that 
is invariant.
From unitarity, one has
Given the dominance of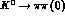 
decay, one
obtains the relation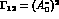 
. From eqs.
(11) and (16), one has
where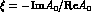 
. In the Cabibbo--Kobayashi--Maskawa
phase convention,
the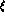 
contribution is small and can be safely neglected.
To make contact with the experiments, one defines the two amplitude ratios
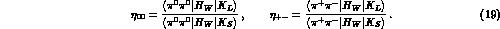
Neglecting small terms, one has
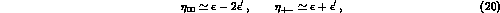
namely
cm
Expressing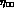 
and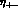 
in terms of the corresponding
widths
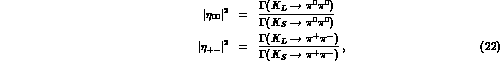
eq. (21) gives the
CP-violation parameters in terms of measurable quantities. Notice that
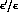is approximately
real, since
experimentally 
.
