Capitolo 245. LaTeX: ambienti matematici
Come avviene per TeX, anche LaTeX distingue una modalità di composizione normale, da una modalità matematica. A differenza di TeX, esistono degli ambienti speciali per la dichiarazione della modalità matematica, ma è ancora ammissibile l'uso del simbolo $ e di $$ per individuare l'inizio e la fine degli ambienti matematici.
Molto di quanto già descritto a proposito di TeX (capitolo 235), vale ovviamente anche per la composizione matematica di LaTeX. Pertanto, alcuni dettagli non vengono descritti nuovamente in questo capitolo.
La gestione degli ambienti matematici può essere ancora più raffinata con l'utilizzo del pacchetto amsmath (\usepackage{amsmath}); tuttavia qui non viene descritto il suo utilizzo.
245.1 Definizione della modalità matematica
La modalità matematica si può definire con LaTeX in diversi modi. Anche con LaTeX si distingue se la composizione matematica vada inserita nell'ambito del testo normale, oppure in un blocco indipendente. L'elenco seguente riepiloga le istruzioni necessarie a delimitare gli ambienti matematici:
|
| compone il testo matematico nel blocco già esistente; |
|
| compone il testo matematico in un blocco separato; |
|
| compone il testo matematico in un blocco separato, annotando sul bordo il numero dell'equazione. |
Come si vede dall'elenco, vengono offerte delle alternative per ottenere lo stesso tipo di ambiente. Vengono mostrati due esempi molto semplici, già apparsi nel capitolo riferito a TeX, che riguardano l'inserimento di una formula nel testo normale e la sua separazione in un blocco a sé stante:
Se $R$ è il ritardo di ogni singola consegna, $T$
è il tempo a disposizione per la consegna, $I$ è il valore
della merce, il ritardo medio si esprime come
\begin{math}{\sum {R \over T} \cdot I}\over{\sum I}\end{math}.
|
|
Se $R$ è il ritardo di ogni singola consegna, $T$
è il tempo a disposizione per la consegna, $I$ è il valore
della merce, il ritardo medio si esprime secondo la formula
seguente:
\begin{displaymath}{\sum {R \over T} \cdot I}\over{\sum I}\end{displaymath}
|
|
A parte le situazioni normali, merita attenzione l'ambiente equation, con il quale si può inserire un'equazione in un blocco separato, al quale si può fare riferimento tramite un'etichetta. Si osservi l'esempio:
L'equazione \ref{ritardo-medio} mostra in che modo si calcola il ritardo
medio, dove $R$ è il ritardo di ogni singola consegna, $T$ è il tempo a
disposizione per la consegna e $I$ è il valore della merce.
\begin{equation}\label{ritardo-medio}
{\sum {R \over T} \cdot I}\over{\sum I}
\end{equation}
|
|
245.2 Spazi orizzontali e punteggiatura
LaTeX si comporta nello stesso modo di TeX a proposito della spaziatura orizzontale negli ambienti matematici. In pratica, gli spazi orizzontali vengono ignorati, a meno che si usino comandi appositi per inserirli:
| Sequenza | Significato |
| \qquad | Due quadratoni. |
| \quad | Un quadratone. |
| \<SP> | Uno spazio «normale». |
| $\;$ | Uno spazio spesso (5/8 di quadratone). |
| $\>$ | Uno spazio medio (2/9 di quadratone). |
| $\.$ | Uno spazio molto sottile (1/6 di quadratone). |
| $\!$ | Uno spazio negativo (-1/6 di quadratone). |
Per inserire del testo descrittivo all'interno di un ambiente matematico, lo si può delimitare in una scatola orizzontale, con il comando \makebox, o più semplicemente con \mbox:
$prima durante e dopo$\par
$prima \mbox{ durante } e dopo$\par
|
Come si può intendere, si vuole isolare e spaziare la parola «durante» rispetto al resto, mostrandola con caratteri normali.
|
Anche la spaziatura attorno ai simboli di punteggiatura funziona esattamente come con TeX puro e semplice. L'esempio seguente riassume i casi principali:
$123456.7890$\par
$123456,7890$\par
$123456{,}7890$\par
$123456;7890$\par
$123456:7890$\par
$123456:=7890$\par
$123456\colon 7890$\par
|
|
245.3 Caratteri e simboli
LaTeX è più ricco di simboli rispetto a TeX, se si utilizza il pacchetto latexsym:
\usepackage{latexsym}
|
Le tabelle che seguono riepilogano i simboli a disposizione, inclusi quelli provenienti dal pacchetto latexsym.
Tabella 245.3. Accenti nell'ambiente matematico.

Tabella 245.4. Lettere greche.

Tabella 245.5. Simboli matematici comuni.

Tabella 245.6. Operatori binari comuni.

Tabella 245.7. Operatori di relazione.

Tabella 245.8. Frecce.

Tabella 245.9. Ellissi.

Tabella 245.10. Altri simboli matematici.

245.4 Delimitatori
LaTeX dispone degli stessi delimitatori di TeX, mantenendo la disponibilità dei comandi \big* e \Big* per gli ingrandimenti controllati. La tabella seguente serve a richiamare l'uso di questi delimitatori, tenendo conto che l'uso dei comandi \big* e \Big* può essere esteso anche oltre gli esempi mostrati.
Tabella 245.11. Delimitatori.

Esiste comunque la possibilità di usare comandi \big* \Big*, senza la lettera l o r che specifica trattarsi di un delimitatore sinistro o destro:

LaTeX offre anche qualche delimitatore speciale; precisamente delle parentesi graffe orizzontali, da usare sopra o sotto qualcosa:
| Comando | Significato |
|
| sovrappone una parentesi graffa sopra il testo; |
|
| sovrappone una parentesi graffa sopra il testo; |
Sono ancora validi con LaTeX i comandi \overline e \underline, per sopralineare e sottolineare nell'ambiente matematico.
245.5 Modifica delle caratteristiche del carattere
Anche con LaTeX sono disponibili i comandi che permettono di controllare la dimensione del carattere negli ambienti matematici. In ordine decrescente, si tratta di: \displaystyle, \textstyle, \scriptstyle e \scriptscriptstyle.
Viene mostrato un esempio già apparso a proposito di TeX:
$$x+{y\over x+{y\over x+{y\over x+{y\over x+{y\over z}}}}}$$\par
$$x+{y\over \displaystyle x+{y\over \displaystyle x+{y\over \displaystyle
x+{y\over \displaystyle x+{y\over z}}}}}$$\par
|
|
A differenza di TeX, LaTeX aggiunge dei comandi cumulabili, anche per la definizione dello stile e della forma del carattere matematico. Nella sezione 239.3 è già stato trattato questo argomento, comunque viene riportato nuovamente l'elenco di questi comandi:
|
| testo matematico normale; |
|
| tondo; |
|
| neretto; |
|
| lineare; |
|
| dattilografico; |
|
| corsivo; |
|
| calligrafico; |
|
| maiuscoletto; |
245.6 Espressioni varie
LaTeX consente di usare i comandi per la realizzazione di frazioni e simili, già disponibili con TeX:
-
$${x+y \over z}$$
-
$${x \over y+z}$$
-
$${a \over x} + {b \over x} = {a+b \over x}$$
-
$${x+y \atop z}$$
-
$${x+y \choose z}$$
-
$${x+y \above 1mm z}$$
Inoltre, LaTeX mette a disposizione un comando aggiuntivo per le frazioni, che forse può risultare comodo in alcune situazioni:
|
| frazione normale. |
Gli apici e i pedici funzionano con LaTeX esattamente come in TeX:
-
$$10^2$$

-
$$10^{20}$$
-
$$10^{-2}$$
-
$$x^a_b$$

-
$$x^{y^z}$$
-
$\sum_{x=0}^n x^3$
-
$$\sum_{x=0}^n x^3$$
-
$$\int_0^n f(x)$$

-
$\lim_{n\to 0} {1 \over n} = \infty$
-
$$\lim_{n\to 0} {1 \over n} = \infty$$
Per ottenere una radice, LaTeX utilizza il comando \sqrt, che però si comporta in modo leggermente diverso da TeX:
|
| produce la radice n dell'argomento indicato. |
Seguono alcuni esempi:
-
$$\sqrt{x^2+y^2}$$
-
$$\sqrt[3]{8}$$
-
$$\sqrt{x+y \over z}$$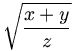
-
$$x^{\sqrt{y}}$$
LaTeX mette a disposizione gli stessi comandi di TeX per la scrittura dei nomi delle funzioni (sezione 235.10). Tuttavia, se si desidera scrivere il nome di una funzione in modo differente, lo si può inserire in una scatola orizzontale:
$$\mbox{sen}(2x)$$
|
Per sovrapporre qualcosa si può usare il comando \stackrel:
$$\stackrel{a}{B}$$
|
245.7 Matrici e sistemi di equazioni
Con LaTeX si rappresentano le matrici in modo molto simile alle tabelle:
\begin{array}{definizione_delle_colonne}
testo & testo [& testo]... \\
[testo & testo [& testo]... \\]
...
\end{array}
La definizione delle colonne avviene, come per l'ambiente tabular, attraverso una stringa composta da tre lettere possibili:
|
| rappresenta una colonna il cui contenuto deve essere allineato a sinistra; |
|
| rappresenta una colonna il cui contenuto deve essere allineato a destra; |
|
| rappresenta una colonna il cui contenuto deve essere allineato al centro. |
Comunque, come nell'ambiente tabular, è possibile anche inserire il simbolo | per ottenere una linea verticale e si può usare il comando \hline per inserire una linea orizzontale.
Segue un esempio molto semplice:
$$\left (
\begin{array}{cc|c}
a & b & c \\
d & e+f & g \\
\hline
h & i & j \\
\end{array}
\right )$$
|
Come si può osservare, l'ambiente array crea la tabella in cui vanno inseriti gli elementi della matrice, mentre la delimitazione esterna deve essere aggiunta espressamente:
|
Trattandosi di una matrice, l'ambiente array si presta in pratica anche per realizzare un sistema di equazioni; è sufficiente regolare correttamente l'allineamento delle colonne, come nell'esempio seguente:
$$|x| =
\bigg \{
\begin{array}{rl}
x & x \geq 0 \\
-x & x \leq 0 \\
\end{array}
$$
|
|
L'ambiente array può essere usato in pratica nello stesso modo di tabular, consentendo così la realizzazione di schemi più complessi di quanto mostrato in questa sezione. Eventualmente si consulti la sezione 243.2.
Tuttavia, esiste un ambiente speciale per elencare delle equazioni allineate a cui poter fare riferimento; si tratta di eqnarray:
\begin{eqnarray}
testo & testo & testo \\
testo & testo & testo \\
...
\end{eqnarray}
In pratica, si tratta di una tabella in cui si presuppone la presenza di tre colonne, allineate rispettivamente a sinistra, al centro e a sinistra. Sarebbe semplicissimo realizzare questo con l'ambiente array, ma la differenza sta nel fatto che ogni riga viene numerata in qualità di equazione. Si osservi l'esempio, in cui si inseriscono anche delle etichette che poi consentono di farvi riferimento:
\begin{eqnarray}
x & = & 2y \label{equazione_xy} \\
y & = & 3z \label{equazione_yz}
\end{eqnarray}
L'equazione \ref{equazione_xy} dice che... mentre l'equazione
\ref{equazione_yz} fa riferimento a...
|
Si osservi il fatto che l'ultima riga della matrice non è terminata con il simbolo \\, perché diversamente si otterrebbe un'equazione in più, numerata, anche se invisibile:
|
|
Ancora più importante è notare che l'ambiente eqnarray viene dichiarato in un contesto normale, ma delimita un ambiente matematico particolare. |
Eventualmente, per evitare di numerare una certa riga, si può usare il comando \nonumber; inoltre, se si aggiunge un asterisco al nome dell'ambiente, non viene mostrata la numerazione di alcuna equazione:
\begin{eqnarray*}
x & = & 2y \label{equazione_xy} \\
y & = & 3z \label{equazione_yz}
\end{eqnarray*}
L'equazione \ref{equazione_xy} dice che... mentre l'equazione
\ref{equazione_yz} fa riferimento a...
|
|
245.8 Teoremi, corollari e dichiarazioni simili
LaTeX ha una gestione sofisticata delle dichiarazioni riconducibili a teoremi, corollari e simili. Si parte dalla dichiarazione di un ambiente, al quale si associa un contatore, in modo tale da non porre limitazioni al genere di dichiarazioni che si vogliono gestire.
Inizialmente si definisce il tipo di contesto a cui appartiene un certo gruppo di dichiarazioni:
\newtheorem{ambiente}{Titolo}[contatore_di_riferimento]
\newtheorem{ambiente}[ambiente_collegato]{Titolo}
La seconda delle due forme permette di definire un ambiente la cui numerazione deve seguire quella di un altro già definito. In questo senso, nel campo indicato come ambiente_collegato, va messo il nome di quello già esistente.
Per cominciare, si osservi l'esempio seguente, senza l'indicazione di alcun contatore di riferimento:
\newtheorem{teorema}{Teorema}
|
In questo modo si dichiara l'ambiente teorema, con il titolo «Teorema», assieme al contatore teorema (a cui si accede facilmente con il comando \theteorema, creato implicitamente), usato in modo trasparente.
|
Nel dichiarare un ambiente di questo tipo, occorre evitare di usare nomi giù usati da LaTeX. |
Dopo la definizione dell'ambiente teorema, si può usare in pratica questo ambiente; per esempio così:
\begin{teorema}
In teoria, non c'è differenza tra pratica e teoria.
\end{teorema}
\begin{teorema}
In pratica, la teoria è diversa dalla pratica.
\end{teorema}
|
Dal risultato della composizione si può osservare che il titolo, ovvero la parola «Teorema», viene messo in evidenza con un carattere nero, assieme al numero del contatore; subito dopo appare il testo del teorema in un carattere corsivo:
|
Nella definizione dell'ambiente teorema era stato omesso il contatore di riferimento, pertanto il conteggio dei teoremi parte da uno e prosegue di conseguenza. Si osservi invece l'esempio seguente, che presuppone un documento di tipo article:
\newtheorem{teorema}{Teorema}[section]
|
In questo modo, si ottiene una numerazione subordinata al contatore section, ovvero alla sequenza delle sezioni:
\section{Alcuni teoremi interessanti}
\begin{teorema}
In teoria, non c'è differenza tra pratica e teoria.
\end{teorema}
\begin{teorema}
In pratica, la teoria è diversa dalla pratica.
\end{teorema}
\section{Un'altra sezione}
\begin{teorema}
Un altro teorema.
\end{teorema}
|
Si può osservare che il numero mostrato dopo il titolo è strutturato, essendo composto da un prefisso che contiene il numero della sezione e da un suffisso che costituisce il numero relativo all'ambito della sezione:
|
Con questa tecnica della dipendenza da un altro contatore, si possono costruire dei corollari la cui numerazione dipende dal teorema appena enunciato. Nell'esempio seguente si mostra anche la definizione degli ambienti usati:
\newtheorem{teorema}{Teorema}[section]
\newtheorem{corollario}{Corollario}[teorema]
\section{Alcuni teoremi e corollari interessanti}
\begin{teorema}
In teoria, non c'è differenza tra pratica e teoria.
\end{teorema}
\begin{corollario}
Bla bla bla bla.
\end{corollario}
\begin{teorema}
In pratica, la teoria è diversa dalla pratica.
\end{teorema}
\begin{corollario}
Bla bla bla bla.
\end{corollario}
|
|
Volendo invece usare una numerazione unica, sia per i teoremi, sia per i corollari, si può usare la seconda forma per la definizione dell'ambiente:
\newtheorem{teorema}{Teorema}[section]
\newtheorem{corollario}[teorema]{Corollario}
...
|
Ecco il risultato seguendo l'ultimo esempio già mostrato:
|
Naturalmente si possono definire anche ambienti di tipo diverso, a seconda delle esigenze; quello che conta è non usare nomi che possono creare conflitti per LaTeX.
Dal momento che queste definizioni sono numerate, diventa importante potervi fare riferimento. Per questo è necessario dichiarare un'etichetta con il comando \label all'interno dell'ambiente:
\newtheorem{teorema}{Teorema}[section]
\section{Alcuni teoremi e corollari interessanti}
\begin{teorema} \label{teorema-della-teoria}
In teoria, non c'è differenza tra pratica e teoria.
\end{teorema}
Purtroppo, il teorema \ref{teorema-della-teoria} viene confutato dal
teorema \ref{teorema-della-pratica}:
\begin{teorema} \label{teorema-della-pratica}
In pratica, la teoria è diversa dalla pratica.
\end{teorema}
|
|
daniele @ swlibero.org















