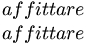Capitolo 235. TeX: ambienti matematici
Come già accennato in un altro capitolo, TeX distingue tra due modalità di funzionamento: un contesto normale e un contesto matematico. L'ambiente matematico si introduce e si conclude con il simbolo $ e in tale situazione diventano disponibili delle istruzioni che non si possono utilizzare al di fuori di questo ambito, mentre alcune istruzioni che erano disponibili prima non lo sono più.
In questo capitolo, anche se si fa riferimento soltanto all'ambiente matematico, nelle tabelle riassuntive che verranno mostrate a proposito di sequenze di controllo che possono essere usate solo nell'ambiente matematico, queste sequenze di controllo verranno delimitate sempre tra una coppia di $, solo per evidenziare il contesto del loro utilizzo.
235.1 Due situazioni differenti
Esistono due modi di mostrare un'informazione matematica: all'interno di testo normale, oppure in un blocco a parte. Quando si inserisce l'informazione dentro del testo normale, si delimita l'ambiente matematico tra due simboli $, per esempio nel modo seguente:
Se $R$ \`e il ritardo di ogni singola consegna, $T$
\`e il tempo a disposizione per la consegna, $I$ \`e il valore
della merce, il ritardo medio si esprime come
${\sum {R \over T} \cdot I}\over{\sum I}$.
|
In tal caso, come si vede dal risultato della composizione, il testo ne risente, in particolare per lo spazio tra le righe che può essere aumentato.
|
In alternativa, le formule possono essere messe in un blocco separato, come nell'esempio seguente:
Se $R$ \`e il ritardo di ogni singola consegna, $T$ \`e il tempo a
disposizione per la consegna, $I$ \`e il valore della merce, il ritardo
medio si esprime secondo la formula seguente:\par
$${\sum {R \over T} \cdot I}\over{\sum I}$$
|
L'effetto è quello di ottenerle al centro della giustezza, con una spaziatura verticale adeguata rispetto al testo che precede e che segue.
|
Negli esempi è stato mostrato l'uso dell'ambiente matematico anche per delimitare i nomi delle variabili. Ciò permette di mantenere coerenza con la forma mostrata nelle formule.
|
Ciò che viene delimitato in una coppia di $ o di $$, non può essere suddiviso in «righe» differenti (tranne il caso di forme tabellari particolari, come le matrici o i sistemi di equazioni), come avviene per la composizione del testo normale; inoltre, il sorgente non può contenere righe vuote o bianche. In pratica si tratta di un blocco orizzontale compatto e indivisibile. |
235.2 Spazi orizzontali
Si osservi subito l'esempio seguente, in cui si scrive la parola «affittare» all'interno di un ambiente matematico, prima in modo normale, quindi spaziando le lettere:
$affittare$\par $a f f i t t a r e$\par |
Come si può osservare dalla composizione che si ottiene, il risultato è esattamente lo stesso. In pratica non viene più preso in considerazione il legato e gli spazi sono ignorati completamente:
|
Per inserire degli spazi in un ambiente matematico, l'unico modo è quello di usare sequenze di controllo specifiche, che possano essere accettate anche in questo ambiente. La tabella 235.1 riepiloga le sequenze di controllo che possono essere usate in un ambiente matematico per ottenere degli spazi orizzontali. Alcune di queste sequenze sono valide solo in un ambito matematico, pertanto appaiono circoscritte da una coppia di $, in modo da sottolineare questa loro caratteristica.
Tabella 235.1. Sequenze di controllo per ottenere delle spaziature orizzontali in ambito matematico.
| Sequenza | Significato |
| \qquad | Due quadratoni. |
| \quad | Un quadratone. |
| \<SP> | Uno spazio «normale». |
| $\;$ | Uno spazio spesso (5/8 di quadratone). |
| $\>$ | Uno spazio medio (2/9 di quadratone). |
| $\.$ | Uno spazio molto sottile (1/6 di quadratone). |
| $\!$ | Uno spazio negativo (-1/6 di quadratone). |
Per inserire del testo descrittivo all'interno di un ambiente matematico, lo si può delimitare in una scatola orizzontale, con l'istruzione \hbox. Si osservi l'esempio:
$prima durante e dopo$\par
$prima \hbox{ durante } e dopo$\par
|
In questo caso, si vuole isolare e spaziare la parola «durante» rispetto al resto, mostrandola con caratteri normali.
|
235.3 Caratteri e simboli
Nell'ambiente matematico, il testo normale viene composto utilizzando un insieme di caratteri differente rispetto a quello normale, in cui anche la forma è particolare, essendo un tipo speciale di corsivo (si ottiene eventualmente con la macro \mit). Inoltre, sono disponibili dei simboli aggiuntivi, in particolare le lettere greche e altri simboli utili in matematica.
Tra le lettere greche, alcune si ottengono come caratteri dell'insieme normale. Nelle tabelle, quando si vuole sottolineare il fatto che si tratta di lettere scritte utilizzando il carattere tondo normale, si mostra un'istruzione del tipo \hbox{\rm x}, che rappresenta il codice necessario all'inserimento in un ambiente matematico.
Tabella 235.2. Accenti nell'ambiente matematico.

Tabella 235.3. Lettere greche.

Tabella 235.4. Simboli matematici comuni.

Tabella 235.5. Operatori binari comuni.

Tabella 235.6. Operatori di relazione.

Tabella 235.7. Frecce.

Tabella 235.8. Ellissi.

Tabella 235.9. Altri simboli matematici.

Eventualmente, è possibile modificare in modo sistematico il tipo di carattere da usare negli ambienti matematici. Si usano per questo due istruzioni alternative:
\everymath={macro_alternativa}
\everydisplay={macro_alternativa}
La prima si riferisce agli ambienti matematici inclusi nel testo normale, mentre la seconda riguarda gli ambienti che creano un blocco separato dal testo.
La macro alternativa a cui si fa riferimento può essere quella che definisce il tipo di carattere da usare. Si osservi l'esempio seguente:
\everymath={\bf}
\everydisplay={\rm}
la funzione $f(x)$ bla bla bla:
$$y = {{x^2}\over 2}$$
|
Si può vedere nel risultato seguente che nel testo normale si ottiene, mentre nel blocco separato si ha un tondo normale:
|
235.4 Dimensione del testo matematico
Il testo matematico, ovvero i simboli che si usano per le espressioni matematiche, viene dimensionato in modo automatico, salvo l'uso diretto di alcune istruzioni apposite. Le istruzioni sono nell'ordine: \displaystyle, \textstyle, \scriptstyle e \scriptscriptstyle. La prima rappresenta la dimensione più grande, mentre l'ultima genera il carattere più piccolo.
Anche se in condizioni normali non è necessario il controllo diretto della dimensione del testo matematico, è bene conoscere questa possibilità che può rivelarsi utile in presenza di formule particolarmente complesse in cui alcune parti rischiano di diventare troppo piccole per la lettura.
A titolo di esempio viene mostrata una frazione piuttosto articolata, in due modi differenti, anche se le frazioni vengono descritte in un'altra sezione:
$$x+{y\over x+{y\over x+{y\over x+{y\over x+{y\over z}}}}}$$\par
$$x+{y\over \displaystyle x+{y\over \displaystyle x+{y\over \displaystyle
x+{y\over \displaystyle x+{y\over z}}}}}$$\par
|
|
Esiste la possibilità di usare \strut, anche nell'ambito matematico, ma questo non previene la riduzione della dimensione dei caratteri. Viene mostrato lo stesso esempio in cui si controlla lo spazio verticale disponibile con l'aiuto di \strut:
\hsize=14cm
$$x+{y\over \strut x+{y\over \strut x+{y\over \strut
x+{y\over \strut x+{y\over z}}}}}$$\par
|
|
235.5 Punteggiatura
Dal momento che nell'ambiente matematico non si tiene conto degli spazi inseriti nel testo, lo spazio attorno ai segni di punteggiatura è gestito automaticamente. Si può osservare l'esempio seguente:
$123456.7890$\par
$123456,7890$\par
$123456:7890$\par
$123456;7890$\par
$123456{,}7890$\par
|
Come si può intuire, se si vuole usare la virgola come separatore della parte intera da quella rimanente, occorre delimitarla in un gruppo a sé stante, per evitare che gli sia aggiunto uno spazio superfluo alla sua destra.
|
Un discorso particolare va fatto per i due punti, che possono servire per indicare una divisione, oppure un assegnamento. Si osservi l'esempio seguente in cui si riprende un pezzo di quanto già mostrato:
$123456:7890$\par $123456:=7890$\par $123456\colon 7890$\par |
In pratica, per ottenere i due punti «normali», a cui segue un po' di spazio, si deve usare l'istruzione \colon.
|
235.6 Frazioni e simili
Le frazioni si indicano solitamente in uno dei due modi seguenti:
numeratore/denominatore
numeratore \over denominatore
Il secondo modo è quello più gradevole esteticamente. È importante osservare che l'istruzione \over interviene su tutto il gruppo in cui è contenuta. Si osservino gli esempi seguenti:
-
$${x+y \over z}$$
-
$${x \over y+z}$$
-
$${a \over x} + {b \over x} = {a+b \over x}$$
Oltre alle frazioni vere e proprie, ci sono altre situazioni simili:
x \atop y
x \choose y
x \above spessore y
Nel primo caso, si ottiene la sovrapposizione di x sopra y, senza la linea orizzontale tipica di una frazione; nel secondo si ottiene la stessa cosa, ma il tutto viene anche racchiuso tra parentesi; nell'ultimo caso, si ottiene una cosa simile alla frazione, dove si specifica lo spessore della linea di separazione. Seguono alcuni esempi:
-
$${x+y \atop z}$$
-
$${x+y \choose z}$$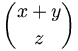
-
$${x+y \above 1mm z}$$
Si osservi che anche in questo caso, le istruzioni mostrate spezzano il gruppo in cui sono inserite, pertanto è necessario racchiudere l'espressione tra parentesi graffe.
La dimensione del testo che si trova a essere spezzata con queste istruzioni viene ridotta automaticamente. Se si vuole evitare questo comportamento, si possono usare le istruzioni già descritte per il controllo esplicito della dimensione.
235.7 Apici e pedici
I pedici e gli apici si ottengono con i simboli _ e ^ rispettivamente, che intervengono sul carattere oppure sul raggruppamento successivo:
x_pedice
x^apice
Si osservino gli esempi successivi, in particolare per quanto riguarda la necessità o meno di raggruppare ciò che va messo ad apice o a pedice:
-
$$10^2$$

-
$$10^{20}$$
-
$$10^{-2}$$
-
$$x^a_b$$

-
$$x^{y^z}$$
-
$\sum_{x=0}^n x^3$
-
$$\sum_{x=0}^n x^3$$
-
$$\int_0^n f(x)$$

-
$\lim_{n\to 0} {1 \over n} = \infty$
-
$$\lim_{n\to 0} {1 \over n} = \infty$$
235.8 Radici
Le radici si possono ottenere attraverso due modi differenti, a seconda che si tratti delle radici quadrate comuni, oppure di radici di altro genere:
\sqrt{contenuto}
\root n \of {contenuto}
Come si intuisce, nel primo caso si ottiene una radice quadrata pura e semplice, mentre nel secondo si dichiara il tipo di radice e successivamente il contenuto. Seguono alcuni esempi.
-
$$\sqrt{x^2+y^2}$$
-
$$\root 3 \of {8}$$
-
$$\sqrt{x+y \over z}$$
-
$$x^{\sqrt{y}}$$
235.9 Sottolineature e sopralineature
Per ottenere delle linee orizzontali sopra o sotto un gruppo di simboli, si usano rispettivamente \overline e \underline:
\overline{contenuto_posto_sotto_la_linea}
\underline{contenuto_posto_sopra_la_linea}
Seguono alcuni esempi:
-
$$\overline{x+y}$$
-
$$\underline{\overline{x+y}}$$
235.10 Funzioni
Quando si vuole fare riferimento al nome standard di una certa funzione matematica, è necessario fare in modo che questo appaia con un carattere diverso dal corsivo matematico, per evitare che si possa confondere con il prodotto di una serie di variabili. Per questa ragione e anche per facilitare la lettura del sorgente TeX, esistono una serie di macro specifiche, con il solo scopo di scrivere il nome della funzione corrispondente usando un carattere tondo normale. La tabella 235.10 elenca brevemente queste macro. Se per qualche ragione si preferiscono dei nomi differenti, si può sempre usare la tecnica del testo nella scatola orizzontale, attraverso l'istruzione \hbox{testo}. Viene mostrato solo qualche esempio di utilizzo:
-
$$\sin(2x)$$

-
$$\cos x$$

-
$$\hbox{sen}(2x)$$
Benché si possa scrivere il nome di una funzione usando la macro \hbox{testo}, TeX offre l'istruzione primitiva \mathop, con cui è possibile definire delle macro aggiuntive da affiancare a quelle standard per la scrittura dei nomi di funzione. Si usa normalmente così:
\def\nome{\mathop{\rm nome}}
Successivamente, sarà sufficiente fare riferimento alla macro \nome per ottenere il nome della funzione relativa in un contesto matematico. Segue l'esempio della dichiarazione e dell'uso della funzione seno, con il nome «sen», assieme al risultato che si ottiene:
\def\sen{\mathop{\rm sen}}
$$\sen(2x)$$
|
|
|
Tabella 235.10. Funzioni standard.

235.11 Delimitatori
In matematica si usano tre tipi di parentesi per delimitare delle sottoespressioni; si tratta notoriamente di parentesi tonde, quadre e graffe. Le stesse parentesi sono disponibili nella modalità matematica di TeX, con la particolarità delle parentesi graffe che devono essere usate attraverso due macro speciali: \{ e \}. In pratica, questa differenza dipende dall'uso speciale che TeX stesso fa di queste parentesi nella sua sintassi.
In condizioni normali, la grandezza delle parentesi usate non è diversa da quella del carattere standard dell'ambiente matematico. Per ottenere parentesi di dimensione maggiore si possono usare alcune macro come \bigl e \bigr, che devono essere seguite immediatamente da una parentesi o da un altro simbolo di delimitazione, allo scopo di ottenerlo più grande del normale. Si osservi l'esempio seguente:
$$\Biggl(\biggl\{\Bigl[\bigl(a+b\bigr)\times c\Bigr]+d\biggr\}\times e\Biggr)$$
|
|
|
In modo più semplice si possono usare le istruzioni \left e \right, che adattano automaticamente le dimensioni delle parentesi o di altri delimitatori, in funzione di ciò che devono contenere. Si osservi l'esempio seguente:
$$\left(\left\{\left[\left(a+b\right)\times c\right]+d\right\}\over e\right)$$
|
|
|
Si osservi che l'altezza delle parentesi non aumenta in presenza di annidamenti successivi, ma soltanto quando la dimensione del contenuto lo richiede.
Tabella 235.11. Delimitatori in sintesi.

La tabella 235.11 mostra un elenco sintetico dei delimitatori e dell'uso delle istruzioni che consentono di ingrandirli. Naturalmente, le istruzioni \left e \right, le macro \bigl, \bigr, fino a Biggl e Biggr, possono essere usate con tutti i tipi di delimitatori matematici disponibili, non solo le parentesi comuni.
235.12 Matrici e sistemi di equazioni
Le matrici si rappresentano in modo molto semplice attraverso le macro \pmatrix e \matrix. La differenza tra le due sta solo nel fatto che nel primo caso si ottiene la delimitazione del contenuto con parentesi tonde di altezza adeguata, mentre nel secondo caso queste devono essere inserite espressamente:
\[p]matrix{
elemento_1_1 [& elemento_1_2]... elemento_1_m \cr
[elemento_2_1 [& elemento_2_2]... elemento_2_m \cr]
...
elemento_n_1 [& elemento_n_2]... elemento_n_m \cr
}
In pratica, il raggruppamento che segue la macro contiene una serie di elementi organizzati in tabella, separati orizzontalmente dal simbolo & e conclusi alla fine di ogni riga da \cr. L'esempio seguente mette a confronto due matrici, realizzate con \pmatrix e \matrix:
$$\pmatrix{
a & b & c \cr
d & e+f & g \cr
h & i & j \cr
}$$
$$\left |
\matrix{
a & b & c \cr
d & e+f & g \cr
h & i & j \cr
}
\right |
$$
|
|
|
Gli elementi della matrice sono spaziati in pratica da uno spazio leggermente elastico, che può essere forzato facilmente. Per esempio, volendo allineare le celle a sinistra, o a destra, basta usare nel lato opposto uno spazio un po' più elastico:
$$\left |
\matrix{
a & b \hfill & c \cr
d & e+f & g \cr
h & \hfill i & j \cr
}
\right |
$$
|
|
|
Naturalmente, queste macro si possono utilizzare anche per qualcosa di diverso dalle matrici, che però è bene appaia incasellato in forma tabellare:
$$|x| =
\bigg \{
\matrix{
x & x \geq 0 \cr
-x & x \leq 0 \cr
}
\right \
$$
|
|
|
Per rappresentare un insieme di «casi», come nella definizione di una funzione, si può usare la macro \cases:
\cases{ espressione & condizione \cr
espressione & condizione \cr
...
espressione & condizione \cr }
Come si vede dal modello sintattico, si distinguono espressioni e condizioni relative: le espressioni sono inserite in un ambiente matematico, mentre le condizioni si trovano in un ambiente di testo normale.
$$f(x) = \cases{
2x & se $x > 0$ \cr
{3x \over 2}+x^2 & se $x < 0$ \cr
}$$
|
|
|
In modo analogo, si usa la macro \eqalign per allineare delle equazioni; in tal caso però, tutti i dati si trovano nell'ambiente matematico:
\eqalign{ espressione & espressione \cr
espressione & espressione \cr
...
espressione & espressione \cr
Dato il nome (Equation align) si intende che l'allineamento debba avere luogo, preferibilmente, in corrispondenza del segno di uguaglianza (o disuguaglianza) usato per abbinare le espressioni. Si osservi l'esempio seguente:
|
|
Infine, un gruppo di espressioni può essere rappresentato su più righe attraverso la macro \displaylines, in modo molto simile a \matrix:
\displaylines{ espressione_1 \cr
espressione_2 \cr
espressione_3 \cr
...
espressione_n \cr }
Viene mostrato un esempio con il risultato che si ottiene:
$$\displaylines{ x+y = y+x \cr
x \times y = y \times x \cr
{x\over y} \not = {y \over x} \cr }
$$
|
|
|
235.13 Dichiarazione di teoremi e corollari
È possibile definire facilmente un teorema o un corollario attraverso la macro \proclaim, secondo lo schema seguente:
\proclaim titolo. definizione
In pratica, si distingue una parte iniziale del testo che segue la macro, fino al primo punto, che viene evidenziato in modo più nero rispetto al resto. Evidentemente, la macro \proclaim viene usata in un ambiente normale (non matematico) e può contenere ambienti matematici nell'ambito della definizione. Si osservi l'esempio seguente:
\proclaim Teorema 1. In teoria, non c'\`e differenza tra pratica e teoria. \proclaim Teorema 2. In pratica, la teoria \`e diversa dalla pratica. |
|
È importante tenere presente che la dichiarazione non può essere più lunga di una riga.
235.14 Equazioni in evidenza
La gestione di equazioni poste nell'ambiente matematico esterno al testo normale, ovvero quello che viene posto in evidenza al centro della giustezza del testo, è particolare.
In modo simile alle matrici, è possibile allineare le equazioni, ma per questo si usa preferibilmente la macro \eqalign, che prevede l'uso di un solo simbolo & per ogni riga. Si osservi l'esempio:
$$\eqalign{
a+b &= c \cr
a+c &= b+c-1 \cr
b+c &= 5 \cr
}$$
|
|
Eventualmente, la macro \equalignno, consente di mostrare qualche informazione in più in prossimità del margine destro. Si ottiene ciò individuando una colonna aggiuntiva nella tabella immaginaria, come si può vedere dall'esempio:
Testo normale, bla bla bla bla bla bla bla bla bla bla bla bla bla bla
bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla.
$$\eqalignno{
a+b &= c & (1) \cr
a+c &= b+c-1 & (2) \cr
b+c &= 5 \cr
}$$
|
|
Nello stesso modo, la macro \lequalignno mostra le annotazioni a sinistra:
Testo normale, bla bla bla bla bla bla bla bla bla bla bla bla bla bla
bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla bla.
$$\leqalignno{
a+b &= c & (1) \cr
a+c &= b+c-1 & (2) \cr
b+c &= 5 \cr
}$$
|
|
Eventualmente, se c'è la necessità di annotare un'espressione che non ha bisogno di essere rappresentata in forma tabellare, si possono usare le istruzioni \eqno e \leqno:
$$a+b = c \eqno (1)$$ $$b+c = b+c-1 \leqno (2)$$ |
|
daniele @ swlibero.org