



Next: 5.8 Determination of and
Up: 5 decays
Previous: 5.6 Previous experiments
The theoretical predictions of 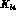 form factors have a long
history which started in the sixties with the current algebra
evaluation of F, G, R and H. For an early review of the
subject and for references to work prior to CHPT we refer the
reader to [34] (see also [35]).
Here we concentrate
on the evaluation of the form factors in the framework of CHPT
[54,55,61,62].
form factors have a long
history which started in the sixties with the current algebra
evaluation of F, G, R and H. For an early review of the
subject and for references to work prior to CHPT we refer the
reader to [34] (see also [35]).
Here we concentrate
on the evaluation of the form factors in the framework of CHPT
[54,55,61,62].
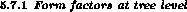
The chiral representation of the form factors at leading order was
originally given by Weinberg [63],
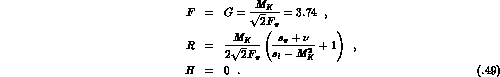
The next-to-leading order corrections are displayed
below, and the later sections contain an estimate of yet higher-order
contributions. Here we note that the
total decay rates which follow from Eq. (5.49) are typically
a factor of two
(ore more) below the data. As an example, consider the channel 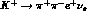 . Using (5.49), the total decay rate
becomes
. Using (5.49), the total decay rate
becomes 1297
sec
1297
sec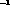 ,
whereas the experimental value is 3160
,
whereas the experimental value is 3160 140 sec
140 sec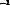 [3].
[3].
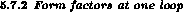
The one-loop result for F [54],[55] may be
written in the form

The contribution
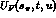 denotes the unitarity correction generated
by the one-loop graphs which appear at order
denotes the unitarity correction generated
by the one-loop graphs which appear at order 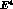 in the low-energy
expansion. Its expression will be given in appendix D.
in the low-energy
expansion. Its expression will be given in appendix D.
The contribution 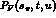 is a polynomial in
is a polynomial in
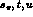 obtained from the tree graphs at order
obtained from the tree graphs at order 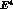 . We
find
. We
find
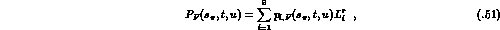
where
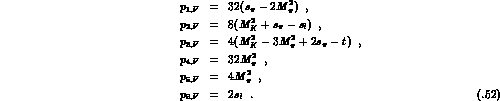
The remaining coefficients 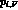 are zero.
are zero.
The contributions 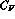 contain
logarithmic terms, independent of
contain
logarithmic terms, independent of 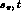 and u:
and u:
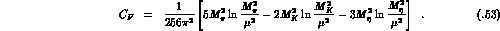
The corresponding decomposition of the form factor G
is [54],[55]
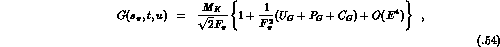
For the expression of  see appendix D.
The polynomials
see appendix D.
The polynomials
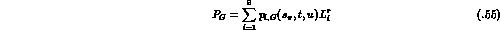
are
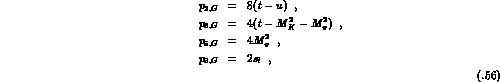
The remaining 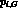 vanish. The logarithms contained in
vanish. The logarithms contained in
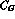 are
are

The form factor R contains a pole part 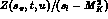 and a
regular piece Q. [Since the axial current acts as an interpolating
field for a kaon, the residue of the pole part is related to
the
and a
regular piece Q. [Since the axial current acts as an interpolating
field for a kaon, the residue of the pole part is related to
the 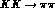 amplitude in the standard manner.] We write
amplitude in the standard manner.] We write
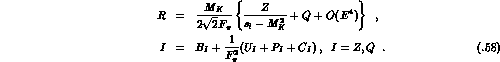
According to (5.49), the Born terms 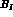 are [63]
are [63]
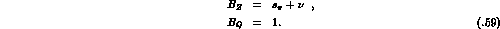
The one-loop corrections have been worked out in Ref. [62].
The unitarity corrections 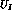 are displayed in the appendix D.
The residues
are displayed in the appendix D.
The residues 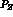 and
and  are
are
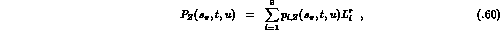
with

The remaining 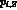 vanish. The logarithms in
vanish. The logarithms in 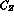 are
are
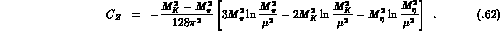
For the nonpole part Q we find:
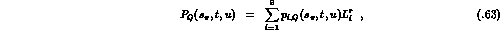
with
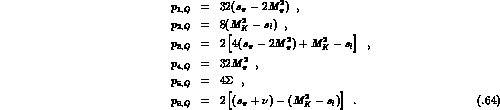
The remaining 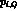 vanish. The logarithms in
vanish. The logarithms in 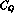 are
are

The first nonvanishing contribution in the chiral expansion of the form factor
H is due
to the chiral anomaly [12].
The prediction is [64]
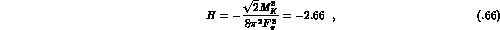
in excellent agreement with the experimental value [53] 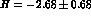 . The
next-to-leading order corrections to H have also been calculated
[65].
If the new low-energy parameters are
estimated using the vector mesons only, these corrections are small.
. The
next-to-leading order corrections to H have also been calculated
[65].
If the new low-energy parameters are
estimated using the vector mesons only, these corrections are small.
The results for F,G and R must satisfy two nontrivial
constraints: i) Unitarity requires that F,G and R contain, in
the physical region  , imaginary
parts governed by S- and P-wave
, imaginary
parts governed by S- and P-wave 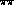 scattering [these
imaginary parts are contained in the functions
scattering [these
imaginary parts are contained in the functions
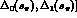 . ii) The scale dependence
of the low-energy constants
. ii) The scale dependence
of the low-energy constants 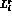 must be compensated by
the scale dependence of
must be compensated by
the scale dependence of 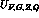 and
and  for all values
of
for all values
of
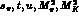 . [Since we work at order
. [Since we work at order  in the
chiral expansion, the
meson masses appearing in the above expressions satisfy the
Gell-Mann-Okubo mass formula.] We have checked that these
constraints are satisfied.
in the
chiral expansion, the
meson masses appearing in the above expressions satisfy the
Gell-Mann-Okubo mass formula.] We have checked that these
constraints are satisfied.
Because the one-loop contributions are rather large, one expects still
substantial corrections from higher orders. In the following
section, we therefore
first estimate the effects from higher orders in
the chiral expansion, using then this improved representation for the form
factors in a comparison with the data.
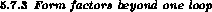
To investigate the importance of higher-order terms, we employ the method
developed in Ref. [66]. It amounts to writing a dispersive
representation of the partial wave amplitudes, fixing the subtraction
constants using chiral perturbation theory. Here, we estimate the
higher-order terms in the S-wave projection of the amplitude 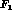 ,
,

because
this form factor plays a decisive role in the determination of 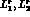 and
and 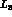 , and it is influenced by S-wave
, and it is influenced by S-wave 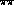 scattering which is known
[67] to produce substantial corrections.
scattering which is known
[67] to produce substantial corrections.

Only the crossing-even part

contributes in the projection (5.67).
The partial wave f has the following analytic properties:
-
At fixed
 , it is analytic in the complex
, it is analytic in the complex 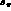 -plane, cut along the real
axis for Re
-plane, cut along the real
axis for Re 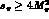 and Re
and Re  .
.
-
In the interval
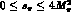 , it is real.
, it is real.
-
In
 , its phase coincides with the
isospin zero S-wave phase
, its phase coincides with the
isospin zero S-wave phase 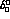 in elastic
in elastic 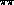 scattering,
scattering,
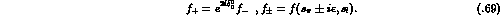
The proof of these properties is standard [68]. Here we only note
that the presence of the cut for  follows from the relations
follows from the relations
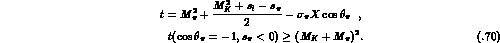
Since  and
and 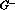 have cuts at
have cuts at 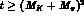 ,
the claim is proven.
,
the claim is proven.
We introduce the Omnès function

where  will be chosen of the order of 1 GeV below.
According to (5.69), multiplication by
will be chosen of the order of 1 GeV below.
According to (5.69), multiplication by 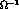 removes the cut in f for
removes the cut in f for 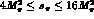 .
Consider now
.
Consider now
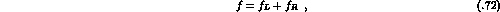
where  has only the left-hand (right-hand) cut, and introduce
has only the left-hand (right-hand) cut, and introduce

Then v has only a right-hand cut, and we may represent it in a dispersive
way,

We expect the contributions from the integral beyond 1 GeV to be small.
Furthermore,
to be small.
Furthermore,  is approximately real between
is approximately real between 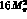 and
1 GeV
and
1 GeV , as a result of which one has
, as a result of which one has
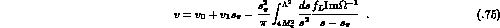
For given  and
and  , the form factor f is finally obtained
from
, the form factor f is finally obtained
from
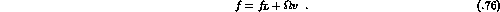
The behaviour of 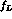 at
at 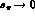 is
governed by the large-|t| behaviour of
is
governed by the large-|t| behaviour of 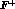 and
and  , see (5.70).
Therefore, instead
of using CHPT to model
, see (5.70).
Therefore, instead
of using CHPT to model 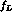 , we approximate the left-hand cut by resonance
exchange. To pin down the
subtraction constants
, we approximate the left-hand cut by resonance
exchange. To pin down the
subtraction constants  and
and
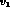 , we require that the threshold expansion of f and
, we require that the threshold expansion of f and 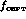 agree
up to and including terms of order
agree
up to and including terms of order 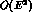 . For a specific choice of
. For a specific choice of 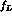 ,
this fixes
,
this fixes  in terms of the quantities which occur in the one-loop
representation of
in terms of the quantities which occur in the one-loop
representation of 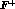 and
and  .
In the case where
.
In the case where 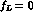 , f has then a particularly simple form at
, f has then a particularly simple form at 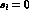 ,
,
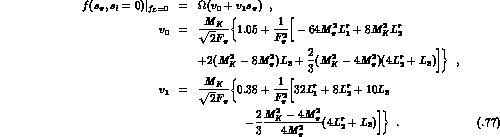
The details of the evaluation of 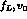 and of
and of  may be found in Ref.
[62].
may be found in Ref.
[62].
In the partial wave f, the effects of the final-state interactions are
substantial, because they are related to the I=0,S-wave 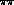 phase
shift. On the other hand, for the leading partial wave in
phase
shift. On the other hand, for the leading partial wave in
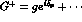 , these effects are reduced, because the phase
, these effects are reduced, because the phase
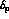 is small at low energies. We find it more difficult to assess an
estimate for the higher-order corrections in this case -- we come back to this
point in the following sections.
is small at low energies. We find it more difficult to assess an
estimate for the higher-order corrections in this case -- we come back to this
point in the following sections.
We add a remark concerning the choice of the subtraction point in the
Omnès function (5.71). To remove the right-hand cut in f, the
modified Omnès function

would do as well, with any value of  . To illustrate the
meaning of
. To illustrate the
meaning of 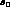 , we consider for simplicity the form factor f
in the case where
, we consider for simplicity the form factor f
in the case where 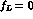 . The choice
. The choice 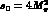 then amounts
to the statement that, at threshold, there are no contributions from two loops
and beyond by fiat. We
consider this to be rather unlikely. (For a different opinion see
[69].) On the other hand, we have checked that our results do not
vary significantly if
then amounts
to the statement that, at threshold, there are no contributions from two loops
and beyond by fiat. We
consider this to be rather unlikely. (For a different opinion see
[69].) On the other hand, we have checked that our results do not
vary significantly if 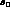 is taken of the order of the pion mass
squared,
is taken of the order of the pion mass
squared, 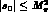 .
.




Next: 5.8 Determination of and
Up: 5 decays
Previous: 5.6 Previous experiments
Carlos E.Piedrafita
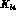 form factors have a long
history which started in the sixties with the current algebra
evaluation of F, G, R and H. For an early review of the
subject and for references to work prior to CHPT we refer the
reader to [34] (see also [35]).
Here we concentrate
on the evaluation of the form factors in the framework of CHPT
[54,55,61,62].
form factors have a long
history which started in the sixties with the current algebra
evaluation of F, G, R and H. For an early review of the
subject and for references to work prior to CHPT we refer the
reader to [34] (see also [35]).
Here we concentrate
on the evaluation of the form factors in the framework of CHPT
[54,55,61,62].
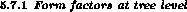
 . Using (
. Using ( ,
whereas the experimental value is 3160
,
whereas the experimental value is 3160 140 sec
140 sec [
[

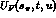 denotes the unitarity correction generated
by the one-loop graphs which appear at order
denotes the unitarity correction generated
by the one-loop graphs which appear at order 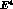 in the low-energy
expansion. Its expression will be given in appendix D.
in the low-energy
expansion. Its expression will be given in appendix D.
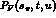 is a polynomial in
is a polynomial in
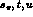 obtained from the tree graphs at order
obtained from the tree graphs at order 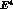 . We
find
. We
find
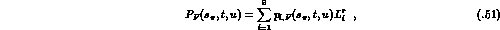
 are zero.
are zero.
 contain
logarithmic terms, independent of
contain
logarithmic terms, independent of  and u:
and u:
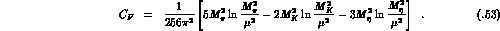
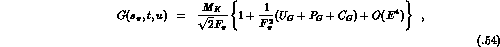
 see appendix D.
The polynomials
see appendix D.
The polynomials
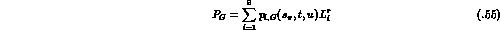
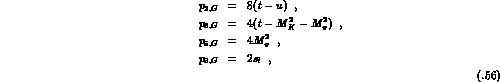
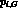 vanish. The logarithms contained in
vanish. The logarithms contained in
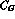 are
are

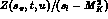 and a
regular piece Q. [Since the axial current acts as an interpolating
field for a kaon, the residue of the pole part is related to
the
and a
regular piece Q. [Since the axial current acts as an interpolating
field for a kaon, the residue of the pole part is related to
the 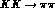 amplitude in the standard manner.] We write
amplitude in the standard manner.] We write
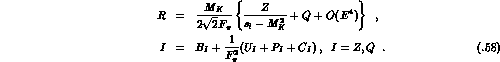
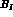 are [
are [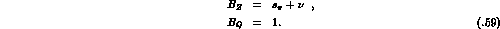
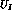 are displayed in the appendix D.
The residues
are displayed in the appendix D.
The residues 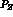 and
and  are
are
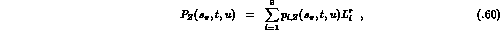

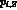 vanish. The logarithms in
vanish. The logarithms in 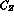 are
are
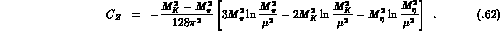
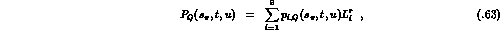
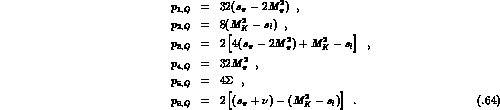
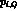 vanish. The logarithms in
vanish. The logarithms in 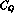 are
are

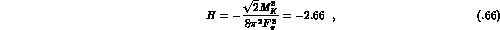
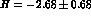 . The
next-to-leading order corrections to H have also been calculated
[
. The
next-to-leading order corrections to H have also been calculated
[ , imaginary
parts governed by S- and P-wave
, imaginary
parts governed by S- and P-wave 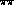 scattering [these
imaginary parts are contained in the functions
scattering [these
imaginary parts are contained in the functions
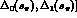 . ii) The scale dependence
of the low-energy constants
. ii) The scale dependence
of the low-energy constants 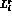 must be compensated by
the scale dependence of
must be compensated by
the scale dependence of 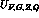 and
and  for all values
of
for all values
of
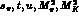 . [Since we work at order
. [Since we work at order  in the
chiral expansion, the
meson masses appearing in the above expressions satisfy the
Gell-Mann-Okubo mass formula.] We have checked that these
constraints are satisfied.
in the
chiral expansion, the
meson masses appearing in the above expressions satisfy the
Gell-Mann-Okubo mass formula.] We have checked that these
constraints are satisfied.
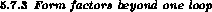
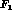 ,
,

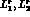 and
and 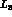 , and it is influenced by S-wave
, and it is influenced by S-wave 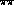 scattering which is known
[
scattering which is known
[

 , it is analytic in the complex
, it is analytic in the complex 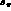 -plane, cut along the real
axis for Re
-plane, cut along the real
axis for Re 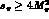 and Re
and Re  .
.
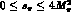 , it is real.
, it is real.
 , its phase coincides with the
isospin zero S-wave phase
, its phase coincides with the
isospin zero S-wave phase 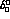 in elastic
in elastic 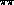 scattering,
scattering,
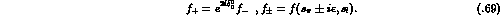
 follows from the relations
follows from the relations
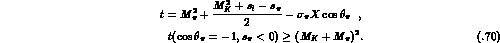
 and
and 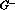 have cuts at
have cuts at 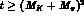 ,
the claim is proven.
,
the claim is proven.
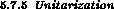

 will be chosen of the order of 1 GeV below.
According to (
will be chosen of the order of 1 GeV below.
According to (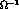 removes the cut in f for
removes the cut in f for 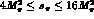 .
Consider now
.
Consider now
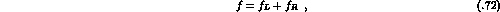
 has only the left-hand (right-hand) cut, and introduce
has only the left-hand (right-hand) cut, and introduce


 to be small.
Furthermore,
to be small.
Furthermore,  is approximately real between
is approximately real between 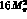 and
1 GeV
and
1 GeV , as a result of which one has
, as a result of which one has
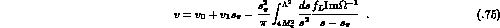
 and
and  , the form factor f is finally obtained
from
, the form factor f is finally obtained
from
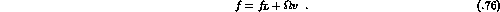
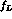 at
at 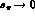 is
governed by the large-|t| behaviour of
is
governed by the large-|t| behaviour of 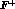 and
and  , see (
, see (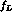 , we approximate the left-hand cut by resonance
exchange. To pin down the
subtraction constants
, we approximate the left-hand cut by resonance
exchange. To pin down the
subtraction constants  and
and
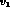 , we require that the threshold expansion of f and
, we require that the threshold expansion of f and 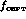 agree
up to and including terms of order
agree
up to and including terms of order 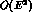 . For a specific choice of
. For a specific choice of 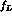 ,
this fixes
,
this fixes  in terms of the quantities which occur in the one-loop
representation of
in terms of the quantities which occur in the one-loop
representation of 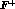 and
and  .
In the case where
.
In the case where 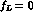 , f has then a particularly simple form at
, f has then a particularly simple form at 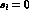 ,
,
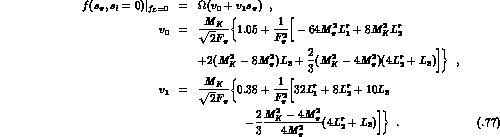
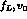 and of
and of  may be found in Ref.
[
may be found in Ref.
[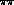 phase
shift. On the other hand, for the leading partial wave in
phase
shift. On the other hand, for the leading partial wave in
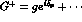 , these effects are reduced, because the phase
, these effects are reduced, because the phase
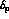 is small at low energies. We find it more difficult to assess an
estimate for the higher-order corrections in this case -- we come back to this
point in the following sections.
is small at low energies. We find it more difficult to assess an
estimate for the higher-order corrections in this case -- we come back to this
point in the following sections.

 . To illustrate the
meaning of
. To illustrate the
meaning of 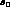 , we consider for simplicity the form factor f
in the case where
, we consider for simplicity the form factor f
in the case where 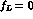 . The choice
. The choice 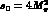 then amounts
to the statement that, at threshold, there are no contributions from two loops
and beyond by fiat. We
consider this to be rather unlikely. (For a different opinion see
[
then amounts
to the statement that, at threshold, there are no contributions from two loops
and beyond by fiat. We
consider this to be rather unlikely. (For a different opinion see
[ is taken of the order of the pion mass
squared,
is taken of the order of the pion mass
squared, 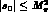 .
.