


Next: 8 Results
Up: Chapter 1 Section 2
Previous: 6 The operators of
In order to estimate 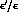 , we have to constrain the CP-violating
phase
, we have to constrain the CP-violating
phase  in the CKM matrix, by using the available experimental
information. To this end, we consider the CP-violating term in the
in the CKM matrix, by using the available experimental
information. To this end, we consider the CP-violating term in the
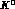 --
--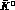 mixing amplitude and the CP-conserving term for
mixing amplitude and the CP-conserving term for
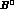 --
--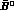 mixing.
In the following, we present all the formulae used in our analysis,
namely the expressions of
mixing.
In the following, we present all the formulae used in our analysis,
namely the expressions of  ,
, 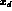 and
and 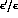 from the
from the
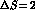 ,
, 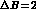 ,
, 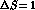 effective Hamiltonian, respectively.
effective Hamiltonian, respectively.
The effective Hamiltonian governing the 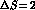 amplitude is given by
amplitude is given by
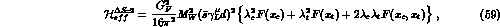
where 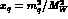 and
the functions
and
the functions 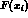 and
and 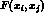 are the so-called
Inami--Lim functions [28], including QCD corrections
[2];
are the so-called
Inami--Lim functions [28], including QCD corrections
[2]; 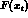 is known at the
next-to-leading order and has been included in our calculation.
From eqs. (18) and (59),
one can derive the CP-violation parameter
is known at the
next-to-leading order and has been included in our calculation.
From eqs. (18) and (59),
one can derive the CP-violation parameter
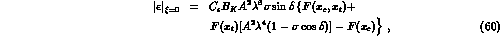
where
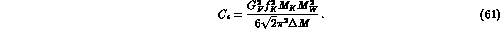
In eq. (60),  ,
, 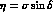 and
and  , A,
, A, 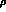 and
and 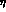 are the
parameters of the CKM matrix in the Wolfenstein parametrization [19].
are the
parameters of the CKM matrix in the Wolfenstein parametrization [19].
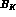 is the renormalization group invariant B-factor, the
definition of which at the leading order is
is the renormalization group invariant B-factor, the
definition of which at the leading order is
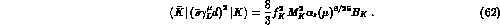
The 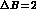 effective Hamiltonian is given by
effective Hamiltonian is given by
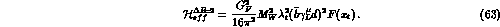
Here 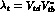 .
From eq. (63), one finds the
.
From eq. (63), one finds the 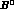 --
-- mixing
parameter
mixing
parameter
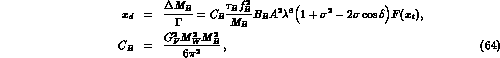
where 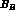 is the B-parameter relevant for
is the B-parameter relevant for  mixing,
the definition of which is analogous to the
mixing,
the definition of which is analogous to the  one.
one.
We can write  as
as

With respect to eq. (14), we have here explicitly written
the isospin-breaking contribution 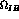 , see for example ref.
[30],
, see for example ref.
[30],
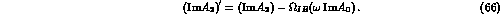
To compute 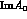 and
and  , we need the
hadronic matrix elements of the operators
, we need the
hadronic matrix elements of the operators 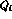 between a kaon and two pions.
Usually they are given in terms of the so-called B-parameters:
between a kaon and two pions.
Usually they are given in terms of the so-called B-parameters:

where the subscripts VIA means that the matrix elements are computed
in the vacuum insertion approximation.
The relevant VIA matrix elements can be expressed in terms
of three quantities
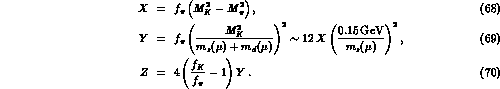
From  , the expressions of
, the expressions of  and
and
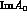 in terms of Wilson coefficients and of the B-parameters
are obtained
in terms of Wilson coefficients and of the B-parameters
are obtained
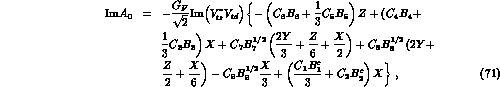
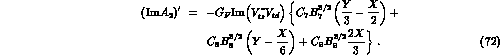
Notice that the matrix elements of the electromagnetic left--right operators
 , which belong to the
, which belong to the 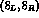 representation of
representation of
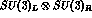 , contain Y and do not vanish in the chiral limit.
, contain Y and do not vanish in the chiral limit.
The evaluation of the B-factors requires a non-perturbative technique.
The Wilson coefficients and the hadronic matrix elements both
depend on the regularization scheme.
In order to cancel this dependence (up to 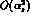 ), it is necessary
to control the matching between the B-parameters and the coefficients at
the next-to-leading order.
Notice that many non-perturbative methods (e.g.
), it is necessary
to control the matching between the B-parameters and the coefficients at
the next-to-leading order.
Notice that many non-perturbative methods (e.g. 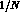 expansion) do not fulfil
this requirement.
expansion) do not fulfil
this requirement.
Two different approaches to the matrix element evaluation have been used
in recent next-to-leading 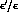 analyses:
analyses:
- In our previous analysis [8,9],
the numerical values of the B-parameters have been taken from lattice
calculations [31].
Suitable renormalization factors are introduced to take into account the
difference between the HV, NDR and lattice regularization
schemes. For those B-parameters not yet computed on the
lattice
 ,
we have made educated guesses, which are discussed in detail in ref.
[9].
,
we have made educated guesses, which are discussed in detail in ref.
[9].
- A phenomenological approach has been implemented in ref. [14],
where
the B-parameters are constrained by using the experimental
information
from CP-conserving processes, by assuming
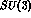 flavour symmetry and
deducing some constraints
relating hadronic matrix elements at the charm threshold.
Unfortunately, there is no way to determine the
most important
B-factors necessary to estimate
flavour symmetry and
deducing some constraints
relating hadronic matrix elements at the charm threshold.
Unfortunately, there is no way to determine the
most important
B-factors necessary to estimate 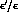 , namely
, namely 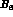 and
and 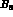 , which
remain essentially unconstrained in this approach.
, which
remain essentially unconstrained in this approach.



Next: 8 Results
Up: Chapter 1 Section 2
Previous: 6 The operators of
Carlos E.Piedrafita
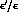 , we have to constrain the CP-violating
phase
, we have to constrain the CP-violating
phase  in the CKM matrix, by using the available experimental
information. To this end, we consider the CP-violating term in the
in the CKM matrix, by using the available experimental
information. To this end, we consider the CP-violating term in the
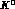 --
--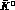 mixing amplitude and the CP-conserving term for
mixing amplitude and the CP-conserving term for
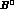 --
--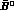 mixing.
In the following, we present all the formulae used in our analysis,
namely the expressions of
mixing.
In the following, we present all the formulae used in our analysis,
namely the expressions of  ,
, 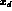 and
and 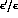 from the
from the
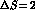 ,
, 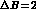 ,
, 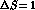 effective Hamiltonian, respectively.
effective Hamiltonian, respectively.
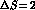 amplitude is given by
amplitude is given by
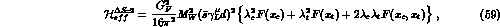
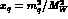 and
the functions
and
the functions 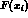 and
and 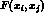 are the so-called
Inami--Lim functions [
are the so-called
Inami--Lim functions [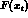 is known at the
next-to-leading order and has been included in our calculation.
From eqs. (
is known at the
next-to-leading order and has been included in our calculation.
From eqs. (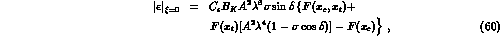
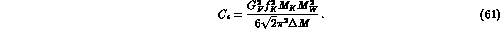
 ,
, 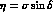 and
and  , A,
, A, 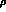 and
and 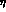 are the
parameters of the CKM matrix in the Wolfenstein parametrization [
are the
parameters of the CKM matrix in the Wolfenstein parametrization [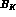 is the renormalization group invariant B-factor, the
definition of which at the leading order is
is the renormalization group invariant B-factor, the
definition of which at the leading order is
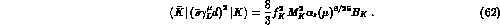
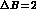 effective Hamiltonian is given by
effective Hamiltonian is given by
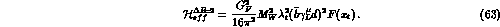
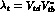 .
From eq. (
.
From eq. (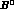 --
-- mixing
parameter
mixing
parameter
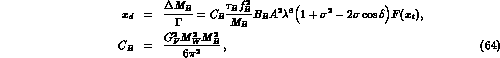
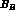 is the B-parameter relevant for
is the B-parameter relevant for  mixing,
the definition of which is analogous to the
mixing,
the definition of which is analogous to the  one.
one.
 as
as

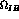 , see for example ref.
[
, see for example ref.
[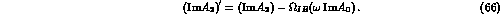
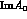 and
and  , we need the
hadronic matrix elements of the operators
, we need the
hadronic matrix elements of the operators 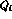 between a kaon and two pions.
Usually they are given in terms of the so-called B-parameters:
between a kaon and two pions.
Usually they are given in terms of the so-called B-parameters:

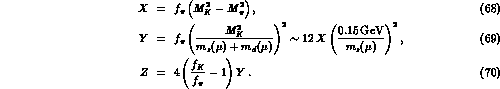
 , the expressions of
, the expressions of 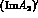 and
and
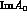 in terms of Wilson coefficients and of the B-parameters
are obtained
in terms of Wilson coefficients and of the B-parameters
are obtained
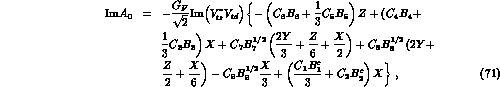
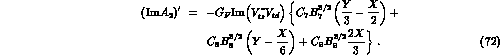
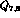 , which belong to the
, which belong to the 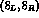 representation of
representation of
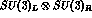 , contain Y and do not vanish in the chiral limit.
, contain Y and do not vanish in the chiral limit.
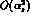 ), it is necessary
to control the matching between the B-parameters and the coefficients at
the next-to-leading order.
Notice that many non-perturbative methods (e.g.
), it is necessary
to control the matching between the B-parameters and the coefficients at
the next-to-leading order.
Notice that many non-perturbative methods (e.g. 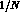 expansion) do not fulfil
this requirement.
expansion) do not fulfil
this requirement.
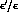 analyses:
analyses:
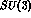 flavour symmetry and
deducing some constraints
relating hadronic matrix elements at the charm threshold.
Unfortunately, there is no way to determine the
most important
B-factors necessary to estimate
flavour symmetry and
deducing some constraints
relating hadronic matrix elements at the charm threshold.
Unfortunately, there is no way to determine the
most important
B-factors necessary to estimate 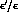 , namely
, namely 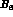 and
and 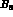 , which
remain essentially unconstrained in this approach.
, which
remain essentially unconstrained in this approach.