



Next: 1.6 Comment on tensor
Up: 1 Radiative decays
Previous: 1.4 Previous experiments
The amplitudes  and
and 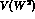 have been worked out in the framework of
various approaches, viz., current algebra, PCAC, resonance exchange,
dispersion relations, ... . For a rather detailed review together with an
extensive list of references up to 1976 see [9]. Here, we concentrate
on the predictions of V, A in the framework of CHPT.
have been worked out in the framework of
various approaches, viz., current algebra, PCAC, resonance exchange,
dispersion relations, ... . For a rather detailed review together with an
extensive list of references up to 1976 see [9]. Here, we concentrate
on the predictions of V, A in the framework of CHPT.
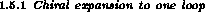
The amplitudes A and V have been evaluated [10,11] in the
framework
of CHPT to one loop. At leading order in the low-energy expansion, one has
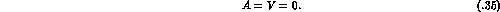
As a consequence of this, the rate is
entirely
given by the IB contribution
at leading order. At the one-loop level, one finds
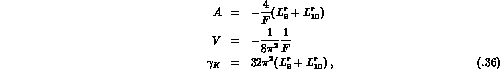
where 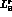 and
and 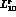 are the renormalized low-energy couplings
evaluated at the scale
are the renormalized low-energy couplings
evaluated at the scale 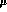 (the combination
(the combination 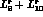 is scale
independent). The vector form factor stems from the Wess-Zumino term
[12] which enters the low-energy expansion at order
is scale
independent). The vector form factor stems from the Wess-Zumino term
[12] which enters the low-energy expansion at order 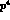 ,
see Ref. [2].
,
see Ref. [2].
Remarks:
- (i)
At this order in the low-energy expansion, the form factors A,V do
not
exhibit any
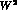 -dependence. A nontrivial
-dependence. A nontrivial  -dependence only occurs at the
next order in the energy expansion (two-loop effect, see the discussion
below). Note that the available analyses of experimental data of
-dependence only occurs at the
next order in the energy expansion (two-loop effect, see the discussion
below). Note that the available analyses of experimental data of 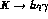 decays [7,4,5,8] use constant form factors
throughout.
decays [7,4,5,8] use constant form factors
throughout.
- (ii) Once the combination
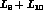 has been pinned down
from other processes, Eq. (1.36) allows one to
evaluate
A,V unambiguously at this order in the low-energy expansion. Using
has been pinned down
from other processes, Eq. (1.36) allows one to
evaluate
A,V unambiguously at this order in the low-energy expansion. Using  and
and  , one has
, one has
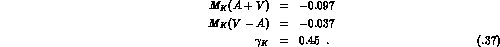
The result for the combination 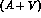 agrees with (1.30) within the
errors,
while
agrees with (1.30) within the
errors,
while 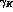 is consistent with (1.32).
is consistent with (1.32).
We display in table 1.3 the branching ratios 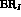 (1.21)
which follow from
the prediction (1.37). These predictions satisfy of course the
inequalities found from experimental data (see table 1.2).
(1.21)
which follow from
the prediction (1.37). These predictions satisfy of course the
inequalities found from experimental data (see table 1.2).
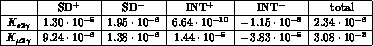
Table 1.3: Chiral
prediction at order 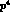 for the branching ratios
for the branching ratios
 . The
cut used in the last column is given in Eq. (1.20).
. The
cut used in the last column is given in Eq. (1.20).
The chiral prediction gives constant form factors at order  . Terms of
order
. Terms of
order 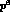 have not yet been calculated. They would, however, generate a
nontrivial
have not yet been calculated. They would, however, generate a
nontrivial  - dependence both in V and A. In order to estimate the
magnitude of these corrections, we consider one class of
- dependence both in V and A. In order to estimate the
magnitude of these corrections, we consider one class of 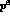 - contributions:
terms which are generated
by vector and axial-vector resonance exchange with
strangeness [9,13],
- contributions:
terms which are generated
by vector and axial-vector resonance exchange with
strangeness [9,13],

where V,A are given in (1.36). We now examine the effect of the
denominators in (1.38) in the region 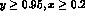 which has been explored in
which has been explored in  [4].
We put
[4].
We put 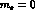 and evaluate the rate
and evaluate the rate
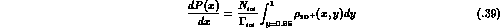
where 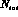 denotes the total number of
denotes the total number of 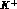 decays
considered, and
decays
considered, and 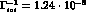 sec.
sec.

Figure 1.3: The rate 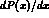 in (1.39), evaluated with the form
factors
(1.38) and
in (1.39), evaluated with the form
factors
(1.38) and
 .
The solid line corresponds to
.
The solid line corresponds to 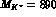 MeV,
MeV, 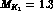 GeV. The dashed line is evaluated with
GeV. The dashed line is evaluated with
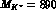 MeV,
MeV, 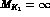 and the dotted line corresponds to
and the dotted line corresponds to
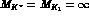 .
The total number of events is also indicated in each case.
.
The total number of events is also indicated in each case.
The function  is displayed in Fig. (1.3) for
three different values of
is displayed in Fig. (1.3) for
three different values of 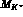 and
and 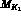 , with
, with
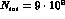 .
The total number of events
.
The total number of events
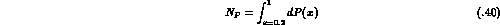
is also indicated in each case. The difference between the dashed and the
dotted line shows that
the nearby singularity in the anomaly form factor influences the decay rate
substantially at low photon energies.
The effect disappears at 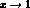 , where
, where 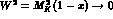 . To minimize the effect of resonance exchange, the
large-x region should thus be
considered. The low-x region, on the other hand, may be used to explore the
. To minimize the effect of resonance exchange, the
large-x region should thus be
considered. The low-x region, on the other hand, may be used to explore the
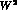 -dependence of V and of A. For a rather exhaustive discussion
of the relevance of this
-dependence of V and of A. For a rather exhaustive discussion
of the relevance of this 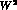 - dependence
for the analysis of
- dependence
for the analysis of 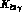 decays we refer the reader to Ref.
[9].
decays we refer the reader to Ref.
[9].




Next: 1.6 Comment on tensor
Up: 1 Radiative decays
Previous: 1.4 Previous experiments
Carlos E.Piedrafita
 and
and 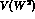 have been worked out in the framework of
various approaches, viz., current algebra, PCAC, resonance exchange,
dispersion relations, ... . For a rather detailed review together with an
extensive list of references up to 1976 see [9]. Here, we concentrate
on the predictions of V, A in the framework of CHPT.
have been worked out in the framework of
various approaches, viz., current algebra, PCAC, resonance exchange,
dispersion relations, ... . For a rather detailed review together with an
extensive list of references up to 1976 see [9]. Here, we concentrate
on the predictions of V, A in the framework of CHPT.
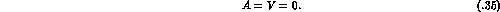
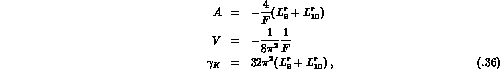
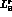 and
and 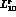 are the renormalized low-energy couplings
evaluated at the scale
are the renormalized low-energy couplings
evaluated at the scale 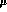 (the combination
(the combination 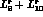 is scale
independent). The vector form factor stems from the Wess-Zumino term
[
is scale
independent). The vector form factor stems from the Wess-Zumino term
[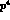 ,
see Ref. [
,
see Ref. [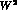 -dependence. A nontrivial
-dependence. A nontrivial  -dependence only occurs at the
next order in the energy expansion (two-loop effect, see the discussion
below). Note that the available analyses of experimental data of
-dependence only occurs at the
next order in the energy expansion (two-loop effect, see the discussion
below). Note that the available analyses of experimental data of 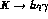 decays [7,4,5,8] use constant form factors
throughout.
decays [7,4,5,8] use constant form factors
throughout.
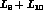 has been pinned down
from other processes, Eq. (1.36) allows one to
evaluate
A,V unambiguously at this order in the low-energy expansion. Using
has been pinned down
from other processes, Eq. (1.36) allows one to
evaluate
A,V unambiguously at this order in the low-energy expansion. Using  and
and  , one has
, one has
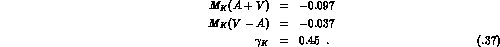
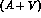 agrees with (
agrees with (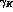 is consistent with (
is consistent with ( (
(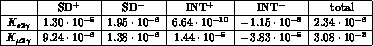
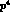 for the branching ratios
for the branching ratios
 . The
cut used in the last column is given in Eq. (
. The
cut used in the last column is given in Eq. (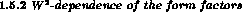
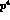 . Terms of
order
. Terms of
order 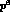 have not yet been calculated. They would, however, generate a
nontrivial
have not yet been calculated. They would, however, generate a
nontrivial  - dependence both in V and A. In order to estimate the
magnitude of these corrections, we consider one class of
- dependence both in V and A. In order to estimate the
magnitude of these corrections, we consider one class of 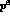 - contributions:
terms which are generated
by vector and axial-vector resonance exchange with
strangeness [
- contributions:
terms which are generated
by vector and axial-vector resonance exchange with
strangeness [
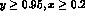 which has been explored in
which has been explored in  [
[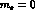 and evaluate the rate
and evaluate the rate
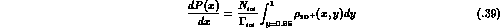
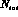 denotes the total number of
denotes the total number of 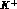 decays
considered, and
decays
considered, and 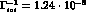 sec.
sec.

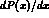 in (
in ( .
The solid line corresponds to
.
The solid line corresponds to 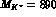 MeV,
MeV, 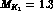 GeV. The dashed line is evaluated with
GeV. The dashed line is evaluated with
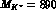 MeV,
MeV, 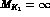 and the dotted line corresponds to
and the dotted line corresponds to
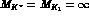 .
The total number of events is also indicated in each case.
.
The total number of events is also indicated in each case.
 is displayed in Fig. (
is displayed in Fig. (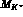 and
and 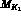 , with
, with
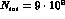 .
The total number of events
.
The total number of events
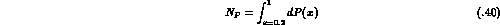
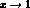 , where
, where 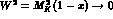 . To minimize the effect of resonance exchange, the
large-x region should thus be
considered. The low-x region, on the other hand, may be used to explore the
. To minimize the effect of resonance exchange, the
large-x region should thus be
considered. The low-x region, on the other hand, may be used to explore the
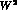 -dependence of V and of A. For a rather exhaustive discussion
of the relevance of this
-dependence of V and of A. For a rather exhaustive discussion
of the relevance of this 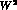 - dependence
for the analysis of
- dependence
for the analysis of 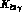 decays we refer the reader to Ref.
[
decays we refer the reader to Ref.
[