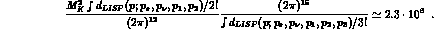
In CHPT, the leading-order contribution is given by the matrix element of the vector current. The corresponding rates are displayed in table (6.1). The smallness of these rates is due to the suppression of phase space. Indeed, consider the ratio of the four- and five-dimensional phase space volumes in the neutral pion channel,
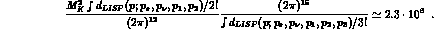
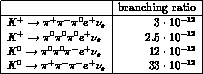
Table 6.1: Rates of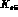 
decays, evaluated from the leading-order term.
It agrees well with the ratio of the corresponding rates at tree level,
(The corresponding ratios for 
are 
and 
for phase space
volumes and decay rates, respectively.)
The contributions at order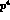 
are due to i) the corrections to the matrix
element of the vector current, and to ii)
the matrix element of the axial current.
The latter stems from the Wess-Zumino-Witten Lagrangian 
. Both
the
local and nonlocal term in the anomalous action contribute. The nonlocal part
is suppressed by the factor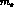 
in the matrix element (in addition to the
phase space suppression just mentioned).
Based on our experience with
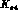decays, we expect the terms of order 
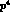to enhance the above rates
by roughly a factor of two to three.