 rest system
rest system
 , the
, the
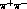 center-of-mass system
center-of-mass system 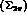 and the
and the
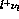 center-of-mass system
center-of-mass system 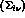 . Then
the variables are
. Then
the variables are
We start with the process (5.1).
The full kinematics of this decay requires five variables.
We will use the
ones introduced by Cabibbo and Maksymowicz [51]. It is
convenient to
consider three reference frames, namely the  rest system
rest system
 , the
, the
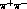 center-of-mass system
center-of-mass system 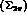 and the
and the
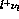 center-of-mass system
center-of-mass system 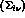 . Then
the variables are
. Then
the variables are
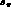 , the effective mass squared of the dipion system,
, the effective mass squared of the dipion system,
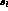 , the effective mass squared of the dilepton system,
, the effective mass squared of the dilepton system,
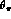 , the angle of the
, the angle of the 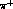 in
in 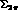 with respect to the dipion line of flight in
with respect to the dipion line of flight in 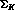 ,
,
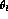 , the angle of the
, the angle of the 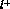 in
in  with respect to the dilepton line of flight in
with respect to the dilepton line of flight in
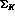 , and
, and
 , the angle between the plane formed by the pions
in
, the angle between the plane formed by the pions
in
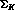 and the corresponding plane formed by the dileptons.
and the corresponding plane formed by the dileptons.
The angles 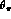 ,
, 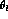 and
and  are displayed in
Fig.
5.1. In order to specify these variables more
are displayed in
Fig.
5.1. In order to specify these variables more

Figure 5.1: Kinematic variables for  decays. The angle
decays. The angle 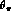 is
defined in
is
defined in 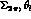 in
in  and
and  in
in
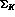 .
.
precisely, let
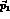 be the three-momentum of the
be the three-momentum of the 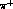 in
in
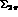 and
and
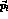 the three-momentum of the
the three-momentum of the 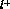 in
in
 .
Furthermore, let
.
Furthermore, let  be a unit vector along the direction
of flight of the dipion in
be a unit vector along the direction
of flight of the dipion in
 , and
, and 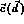 a unit vector along
the projection
of
a unit vector along
the projection
of  perpendicular to
perpendicular to 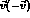 ,
,

The vectors  ,
,  and
and 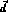 are indicated in Fig. 5.1. Then, one has
are indicated in Fig. 5.1. Then, one has
The range of the variables is
It is useful to furthermore introduce the following combinations of four vectors
together with the corresponding Lorentz invariant scalar products
with
Below we will also use the variables
These are related to 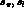 and
and 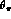 by
by