in terms of the amplitude T in (4.1). The square of the matrix
element, summed over photon and lepton polarizations, is a bilinear form
in the invariant amplitudes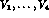 
, 
,
.
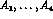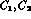Pulling out common factors, we write (4.14) in the form
where SM is the reduced matrix element. For the actual numerical calculations, we have found it useful to employ a tensor decomposition different from the one in Eqs. (4.7) and (4.9)
One advantage is that (4.16) applies equally well to both
charge modes while (4.7) does not.
In the numerical evaluation of the amplitudes, gauge invariance
can of course be used to express three of the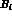 
in terms of the
remaining ones and of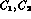 
.
To get some feeling for the magnitude of the various decay rates, let
us first consider the tree level amplitudes to lowest order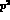 
in
CHPT. With the sign conventions of Ref. [44],
these amplitudes are
[11,45] :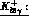 
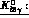
In table 4.1 the corresponding branching ratios
are presented for the four decay modes for
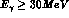and 
.
For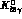 
, the rates are to be understood as
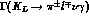. The
number of events correspond to the design values for DA
NE (cf.
App. A ).
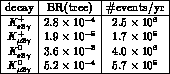
Table 4.1: Branching ratios for tree level amplitudes for 
and 
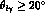in the K rest
frame.
