



Next: 3.6 Comment on tensor
Up: 3 decays
Previous: 3.4 Previous measurements
The theoretical prediction of  form factors has a long history,
starting
in the sixties with the current algebra evaluation of
form factors has a long history,
starting
in the sixties with the current algebra evaluation of  . For
an
early review of the subject and for references to work prior to CHPT
evaluations
of
. For
an
early review of the subject and for references to work prior to CHPT
evaluations
of 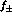 we refer the reader to [34] (see also Ref.[35]).
Here we concentrate on the
evaluation of the form factors in the framework of CHPT. We restrict our
consideration to the isospin symmetry limit
we refer the reader to [34] (see also Ref.[35]).
Here we concentrate on the
evaluation of the form factors in the framework of CHPT. We restrict our
consideration to the isospin symmetry limit 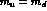 , as a result of which
one has
, as a result of which
one has

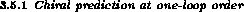
In Ref. [24], the vector current matrix elements 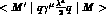 have been calculated up to and
including terms of order
have been calculated up to and
including terms of order 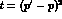 and of order
and of order 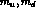 and
and 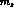 in
the invariant form factors. For reasons which will become evident below, we
consider here, in addition to the
in
the invariant form factors. For reasons which will become evident below, we
consider here, in addition to the 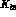 form factors, also
the electromagnetic form factor of the pion
form factors, also
the electromagnetic form factor of the pion
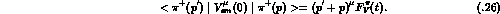
The low-energy representation for  [24,36] and
[24,36] and
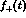 [24] reads
[24] reads


The quantity 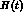 is a loop function
displayed in appendix B. It contains the low-energy constant
is a loop function
displayed in appendix B. It contains the low-energy constant 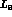 .
The indices attached to
.
The indices attached to 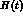 denote the masses running in the loop.
denote the masses running in the loop.
Since 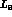 is the only unknown occurring in
is the only unknown occurring in 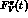 and
in
and
in  , we need experimental information on the slope of one of these two
form factors to obtain a parameter-free low-energy representation of the
other.
, we need experimental information on the slope of one of these two
form factors to obtain a parameter-free low-energy representation of the
other.
The analogous low-energy representation of the scalar form factor is

The function 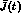 is listed in appendix B, and
is listed in appendix B, and
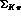 and
and 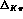 stand for
stand for
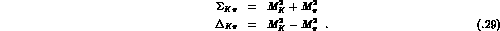
The measured value [26] 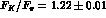 may be used to
obtain a parameter-free prediction of the scalar form factor
may be used to
obtain a parameter-free prediction of the scalar form factor 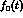 .
.
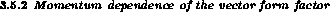
In the spacelike interval 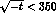 MeV the low-energy representation
(3.27) for the electromagnetic form factor
MeV the low-energy representation
(3.27) for the electromagnetic form factor 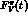 is very well
approximated by the first two terms in the Taylor series expansion
around t=0,
is very well
approximated by the first two terms in the Taylor series expansion
around t=0,
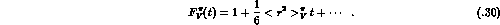
Likewise, the linear approximation

reproduces the low-energy representation (3.27) very
well, see Fig. 3.1.
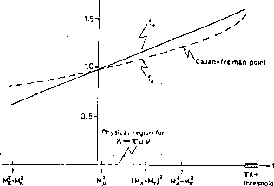
Figure 3.1: The vector and scalar form factors  and
and 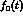 .
.
This is in agreement with the observed Dalitz plot distribution, which is
consistent with a form factor linear in t. The charge radii are
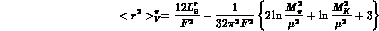
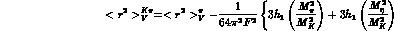
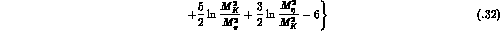
where
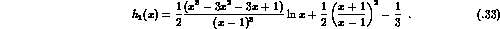
To evaluate these relations numerically, we use the measured charge radius of
the pion:

as input and obtain the prediction
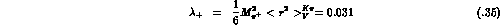
in agreement with
the experimental results (3.22), (3.23)
 .
From this (and from the considerably more detailed discussion in Ref.
[24]), one concludes, in agreement with other
theoretical investigations [38], that the measured charge radii
.
From this (and from the considerably more detailed discussion in Ref.
[24]), one concludes, in agreement with other
theoretical investigations [38], that the measured charge radii
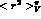 and
and  are consistent with the low-energy
prediction.
are consistent with the low-energy
prediction.
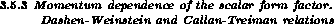
In the physical region of  decay the low-energy representation
(3.28) for the scalar form factor is approximated by the linear
formula
decay the low-energy representation
(3.28) for the scalar form factor is approximated by the linear
formula
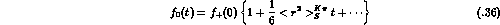
to within an accuracy of 1 %. (See Fig. 3.1). The curvature generated
by higher-order
terms is also expected to be negligible in the physical region of the
decay [24]. For the slope  one obtains
one obtains
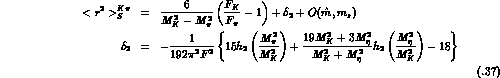
where

This (parameter-free) prediction is a modified version of the
Dashen-Weinstein
relation [39], which results if the nonanalytic contribution
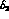 is dropped. Dashen, Li, Pagels and Weinstein [40] were the
first to point out that the low-energy singularities generated by the Goldstone
bosons affect this relation. The modified relation is formulated as a
prediction for the slope of
is dropped. Dashen, Li, Pagels and Weinstein [40] were the
first to point out that the low-energy singularities generated by the Goldstone
bosons affect this relation. The modified relation is formulated as a
prediction for the slope of 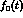 at the unphysical point
at the unphysical point  . Their expression for this slope however has two shortcomings: (i) it
does not account for all corrections of order
. Their expression for this slope however has two shortcomings: (i) it
does not account for all corrections of order 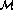 ; (ii) The slope at
; (ii) The slope at
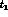 differs substantially from the slope in the physical region of the decay
[24,41], see Fig. 3.2.
differs substantially from the slope in the physical region of the decay
[24,41], see Fig. 3.2.
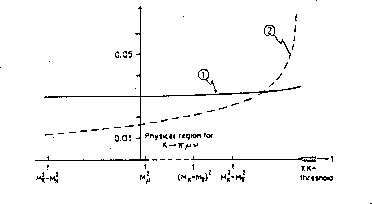
Figure 3.2: The normalized slopes of the vector and the scalar form factors.
Curve 1: the normalized slope 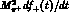 . Curve 2: the
normalized
slope
. Curve 2: the
normalized
slope 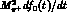 . Near the
. Near the 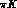 threshold
threshold  ,
the vector form factor behaves as
,
the vector form factor behaves as 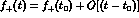 , whereas
, whereas
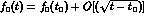 . The slope of the scalar form
factor is therefore singular at
. The slope of the scalar form
factor is therefore singular at 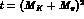 .
.
Algebraically, the correction 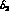 is of the same order in the low-energy
expansion as the term involving
is of the same order in the low-energy
expansion as the term involving 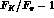 . Numerically, the correction is
however small:
. Numerically, the correction is
however small: 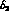 reduces the prediction by 11 %. With
reduces the prediction by 11 %. With 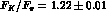 the low-energy theorem (3.37) implies
the low-energy theorem (3.37) implies
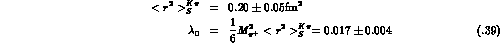
where the error is an estimate of the uncertainties due to higher-order
contributions. The prediction (3.39) is in agreement with the
high-statistics experiment [28] quoted in (3.23) but in
flat disagreement with some of the more recent data listed in
(3.24).
In the formulation of Dashen and Weinstein [39], the Callan-Treiman
relation [42] states
that the scalar form factor evaluated at 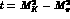 differs from
differs from
 only by terms of order
only by terms of order 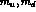 : the quantity
: the quantity
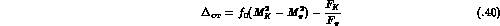
is of order 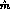 . Indeed, the low-energy
representation (3.28) leads to
. Indeed, the low-energy
representation (3.28) leads to

Numerically,  . The
Callan-Treiman relation should therefore hold to a very high degree of
accuracy. If the form factor is linear from t=0 to
. The
Callan-Treiman relation should therefore hold to a very high degree of
accuracy. If the form factor is linear from t=0 to 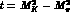 then
the slope must be very close to
then
the slope must be very close to
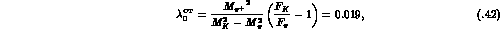
in agreement with (3.39) and with the experimental result of Ref.
[28], but in disagreement with, e.g., the value found in Ref.
[30]. We see no way to reconcile the value 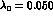 with
chiral symmetry.
with
chiral symmetry.




Next: 3.6 Comment on tensor
Up: 3 decays
Previous: 3.4 Previous measurements
Carlos E.Piedrafita
 form factors has a long history,
starting
in the sixties with the current algebra evaluation of
form factors has a long history,
starting
in the sixties with the current algebra evaluation of  . For
an
early review of the subject and for references to work prior to CHPT
evaluations
of
. For
an
early review of the subject and for references to work prior to CHPT
evaluations
of  we refer the reader to [34] (see also Ref.[35]).
Here we concentrate on the
evaluation of the form factors in the framework of CHPT. We restrict our
consideration to the isospin symmetry limit
we refer the reader to [34] (see also Ref.[35]).
Here we concentrate on the
evaluation of the form factors in the framework of CHPT. We restrict our
consideration to the isospin symmetry limit 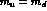 , as a result of which
one has
, as a result of which
one has

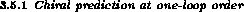
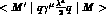 have been calculated up to and
including terms of order
have been calculated up to and
including terms of order 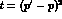 and of order
and of order 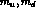 and
and 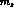 in
the invariant form factors. For reasons which will become evident below, we
consider here, in addition to the
in
the invariant form factors. For reasons which will become evident below, we
consider here, in addition to the 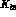 form factors, also
the electromagnetic form factor of the pion
form factors, also
the electromagnetic form factor of the pion
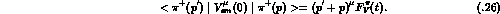
 [
[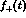 [
[

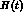 is a loop function
displayed in appendix B. It contains the low-energy constant
is a loop function
displayed in appendix B. It contains the low-energy constant 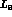 .
The indices attached to
.
The indices attached to 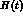 denote the masses running in the loop.
denote the masses running in the loop.
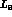 is the only unknown occurring in
is the only unknown occurring in 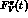 and
in
and
in  , we need experimental information on the slope of one of these two
form factors to obtain a parameter-free low-energy representation of the
other.
, we need experimental information on the slope of one of these two
form factors to obtain a parameter-free low-energy representation of the
other.

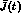 is listed in appendix B, and
is listed in appendix B, and
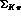 and
and 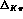 stand for
stand for
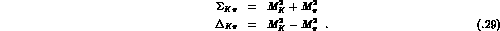
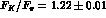 may be used to
obtain a parameter-free prediction of the scalar form factor
may be used to
obtain a parameter-free prediction of the scalar form factor 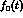 .
.
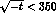 MeV the low-energy representation
(
MeV the low-energy representation
( is very well
approximated by the first two terms in the Taylor series expansion
around t=0,
is very well
approximated by the first two terms in the Taylor series expansion
around t=0,
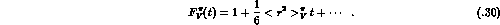


 and
and 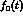 .
.
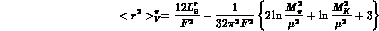
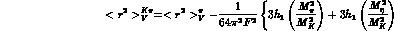
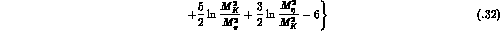
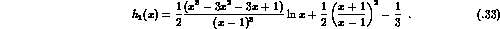

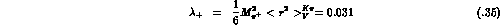
 and
and  are consistent with the low-energy
prediction.
are consistent with the low-energy
prediction.
 decay the low-energy representation
(
decay the low-energy representation
(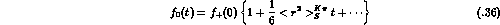
 one obtains
one obtains
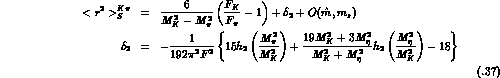

 is dropped. Dashen, Li, Pagels and Weinstein [
is dropped. Dashen, Li, Pagels and Weinstein [ at the unphysical point
at the unphysical point  . Their expression for this slope however has two shortcomings: (i) it
does not account for all corrections of order
. Their expression for this slope however has two shortcomings: (i) it
does not account for all corrections of order 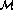 ; (ii) The slope at
; (ii) The slope at
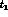 differs substantially from the slope in the physical region of the decay
[
differs substantially from the slope in the physical region of the decay
[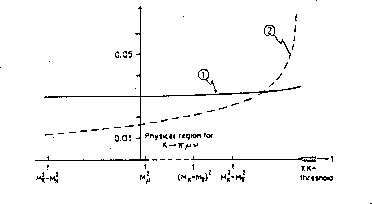
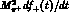 . Curve 2: the
normalized
slope
. Curve 2: the
normalized
slope 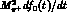 . Near the
. Near the 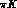 threshold
threshold  ,
the vector form factor behaves as
,
the vector form factor behaves as 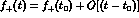 , whereas
, whereas
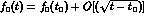 . The slope of the scalar form
factor is therefore singular at
. The slope of the scalar form
factor is therefore singular at 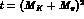 .
.
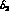 is of the same order in the low-energy
expansion as the term involving
is of the same order in the low-energy
expansion as the term involving 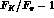 . Numerically, the correction is
however small:
. Numerically, the correction is
however small: 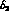 reduces the prediction by 11 %. With
reduces the prediction by 11 %. With 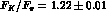 the low-energy theorem (
the low-energy theorem (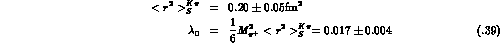
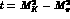 differs from
differs from
 only by terms of order
only by terms of order  : the quantity
: the quantity
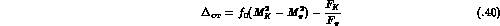
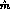 . Indeed, the low-energy
representation (
. Indeed, the low-energy
representation (
 . The
Callan-Treiman relation should therefore hold to a very high degree of
accuracy. If the form factor is linear from t=0 to
. The
Callan-Treiman relation should therefore hold to a very high degree of
accuracy. If the form factor is linear from t=0 to 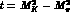 then
the slope must be very close to
then
the slope must be very close to
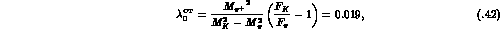
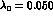 with
chiral symmetry.
with
chiral symmetry.