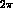The notation for phase space is the one without the factors of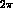 
.
For the decay rate of a
particle with four momentum p into n particles
with momenta 
this is
We use a covariant normalization of one-particle states,
together with the spinor normalization
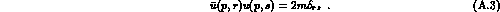
The kinematical function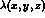 
is defined as
We take the standard model in the current 
current form, i.e.,
we neglect the momentum dependence of the W-propagator. The currents
used in the text are :
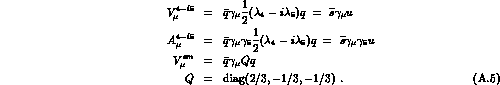
The numerical values used in the programs are the physical masses for the particles as given by the Particle Data Group [3]. In addition we have used the values for the decay constants derived from the most recent measured charged pion and kaon semileptonic decay rates[3,26] :
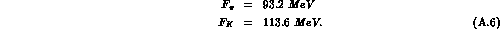
We do not need values for the quark masses. For the processes considered
in this report we can always use the lowest order relations to rewrite
them in terms of the
pseudoscalar meson masses (see Ref. [2]). For the
KM matrix element
we used the central value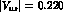 
of Ref. [3].
The numerical values for the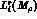 
are those
given in table 1 in Ref. [2].
The number of events quoted for DA
NE are based on a
luminosity of 
,
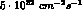which is equivalent [1]
to an annual rate of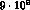 
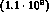tagged
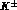
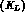(1 year = 
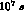assumed).
Whenever we quote a branching ratio for a semileptonic
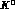decay, it stands for the branching ratio of the corresponding
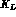decay, e.g.,
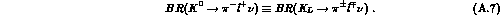
We use the Condon-Shortley phase conventions throughout.