This file contains the following subjects:
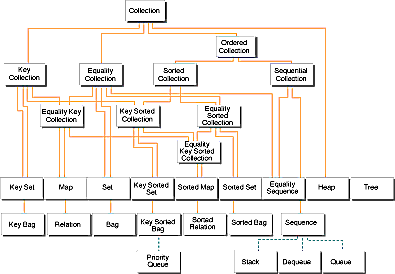
The classes in the Collection Classes are all related through the hierarchy of abstract classes shown in the figure below:

In the figure, abstract collections have a gray shadow, concrete collections have a black shadow, and restricted-access collections have a white shadow. The leaves of the collection hierarchy (those collections that have no derived classes within the hierarchy tree) define the collection for which concrete implementations are provided. The lines in the figure represent an "is-a" relationship from a lower collection to the collection above it. For example, a set is an equality collection, which is a collection.
Dotted lines show a "based-on" relationship, not an actual derivation.
The abstract collection classes represent a concept, and classes derived from it represent implementations of the concept. With abstract classes, you can program to a more generalized interface without knowing what specific collection type your code will operate on. Implementation details can be left for later. For example, when working with a set, you can write your program to use the interfaces of the abstract classes IASet or IAEqualityCollection, rather than the concrete classes ISet, IGSet, ISetAsBstTree, and so on.
The names of the abstract collection classes start with the letters IA.
Each abstract collection type has several possible implementations. Some of these implementations are basic; that is, the collection class is implemented directly as a concrete class. These basic implementations include:
Variant implementations of the same collection behave externally in the same way but may offer improved performance for a particular application, depending on the collection's characteristics. Sets can be implemented, for example, as AVL trees, lists, or hash tables.
Default implementations are provided for every collection. Two default classes are provided for each abstract data type: a class that is instantiated only with the element type (and possibly the key type) and one that is instantiated by passing in element-specific functions. In many cases, you do not need to concern yourself with the choice of implementation. If you choose not to specify one, the Collection Classes will use a reasonable default implementation class.
Each class falls within one of the following categories: concrete, typed implementation, typeless implementation, and abstract. The figure below illustrates the relationships (indicated by arrows) between the categories of classes for the set collection classes. Arrows indicate a relationship between classes:
Overall Structure of Collection Classes
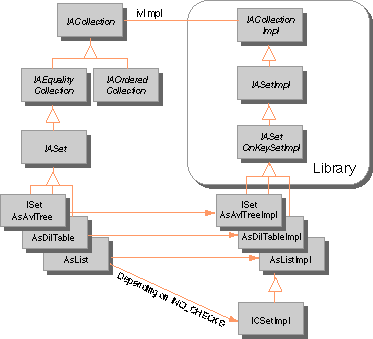
The class ISet uses an AVL tree as the default implementation. The other implementation variants are linked list and diluted table. The three implementation variants ISetAsAvlTree, ISetAsList, and ISetAsDilTable are subclasses of IASet. If you do not want to deal with implementation variants, you can just use the default class ISet.
The Collection Classes achieve a high degree of implementation flexibility by basing several collection class implementations on other abstract classes, rather than by implementing them directly through a concrete implementation variant of the class. This design feature results in an implementation path rather than the selection of an implementation in a single step. The Collection Classes contain type definitions for the most common implementation paths.
The element functions that are needed by a particular implementation depend on all collection class templates that participate in the implementation. While ISet requires at least element equality to be defined, an AVL tree implementation of this set also requires the element type to provide a comparison function. A hash table implementation also requires the element type to have a hash function. The required element functions for all predefined implementation variants are listed for individual collection types.
For a concrete implementation, such as a set based on a key-sorted set that is in turn based on a tabular sequence, these class templates are plugged together so that the elements only need to define the operations that are needed for the specific type of collection being used.
The member functions of the Collection Class Library call other functions to manipulate elements and keys. These functions are called element functions and key-type functions, respectively. Member functions of the Collection Class Library may, for example, use the element's assignment or copy constructors for adding an element, or they may use the element's equality operator for locating an element in the collection.
Polymorphic use of collections differs from polymorphism of the element type. Polymorphic use of collections means that a function can specify an abstract collection type for its argument, for example IACollection, and then accept any concrete collection given as its actual argument. Element polymorphism means that you can use the collections with any elements that provide basic operations like assignment and equality. This section deals with the polymorphic use of collections rather than elements.
Each abstract class is defined by its functions and their behavior. The most abstract view of a collection is a container without any ordering or any specific element or key properties. Elements can be added to a collection, and a collection can be iterated over. A polymorphic function on collections that uses only properties of the most abstract view might be to print all elements.
Collections with more specialized element properties, such as equality or key equality, also provide functions for retrieving element occurrences by a given element or key value. Ordered collections provide the notion of a well-defined ordering of element occurrences, either by an element ordering relation or by explicit positioning of elements within a sequence. Ordered collections define operations for positional element access. Sorted collections provide no further functions, but define a more specific behavior, namely that the elements or their keys are sorted.
The properties represented by abstract collection classes are combined through multiple inheritance. For example, the abstract collection class IAEqualitySortedCollection, for example, combines the properties of element equality and element sorting, which implies being ordered. If a polymorphic function uses IAEqualitySortedCollection as its argument type, the argument will be sorted, and the function can use functions such as contains that are only defined for collections with element equality.
![]()
Introduction to the
Collection Classes
Collection
Characteristics
Ordering of
Collection Elements
Access by Key
Equality
Relation
Uniqueness
of Entries
Flat Collections
Trees
Exceptions
Defined and Used by the Collection Classes
Exception
Causes
Exceptions
Caused by System Failures and Restrictions
Smart Pointers
![]()
Memory
Management with Element Operation Classes
Choosing the
Appropriate Smart Pointer Class
Class Template
Naming Conventions
Possible
Implementation Paths
Choosing One
of the Provided Implementation Variants
Copying and
Referencing Collections
Replacing
the Default Implementation
Instantiating
the Collection Classes
Taking Advantage
of the Abstract Class Hierarchy
Adding and
Overloading Member Functions
